+ - 0:00:00
Notes for current slide
Notes for next slide

We meet today on Treaty 4 lands, the territories of the Cree, Saulteaux (SOH-toh), Dakota, Lakota, Nakoda, and the homeland of the Métis Nation.

Today, these lands continue to be the shared territory of many diverse peoples.

Wibbly Wobbly Timey Wimey Stuff

Gavin Simpson • Kim Hinz • Stefano Mezzini

Department of Biology • November 29th 2019

We meet today on Treaty 4 lands, the territories of the Cree, Saulteaux (SOH-toh), Dakota, Lakota, Nakoda, and the homeland of the Métis Nation.

Today, these lands continue to be the shared territory of many diverse peoples.

Use statistics to learn from data in presence of noise

One way to describe statistics is the principled process by which we learn from data in the presence of noise and uncertainty

Learning from data…?

Why would we want to learn from data?

Estimate parameters for a theoretical model

Lotka-Voltera models of competition between species

Compare theory with observation

What do the data tell us?

If we want to know how theory matches with observation then we might want to see what the data can tell us without imposing too many restrictions or constraints on our statistical model

Progress with little or no theory

We may have little or no theory to work with, so we take an empirical approach which may lead to the development of new theory

unsplash-logoFranki Chamaki

We learn from data because it can highlight our preconceptions and biases

Learning from data

Learning from data could be a simple as fitting a linear regression model...

Or as complex as fitting a sophisticated multi-layered neural network trained on huge datasets or corpora

Learning involves trade-offs

Learning from data involves trade offs

We can have models that fit our data well — low bias — but which are highly variable, or

We can fit models that have lower variance, but these tend to have higher bias, i.e. fit the data less well

A linear regression model is very interpretable but unless the underlying relationship is linear it will have poor fit

Deep learning may fit data incredibly well but the model is very difficult to interpret and understand

Generalized Additive Models


Source: GAMs in R by Noam Ross

GAMs are an intermediate-complexity model

  • can learn from data without needing to be informed by the user
  • remain interpretable because we can visualize the fitted features

GAMs fit wibbly wobbly functions

Heresey, I know, but I prefer my sci-fi more Duffer Brothers than Time Lord

The wibbly wobbly stuff — splines

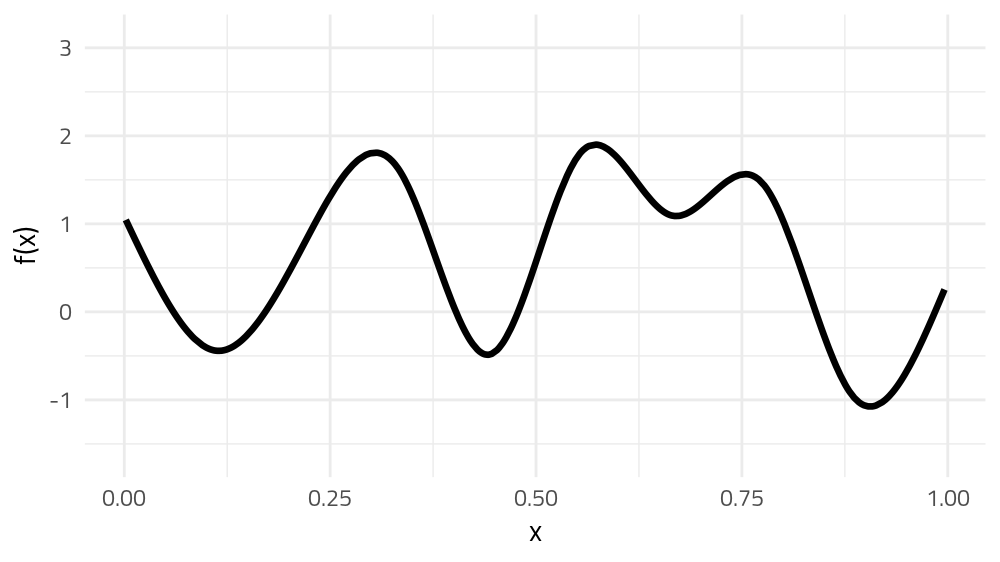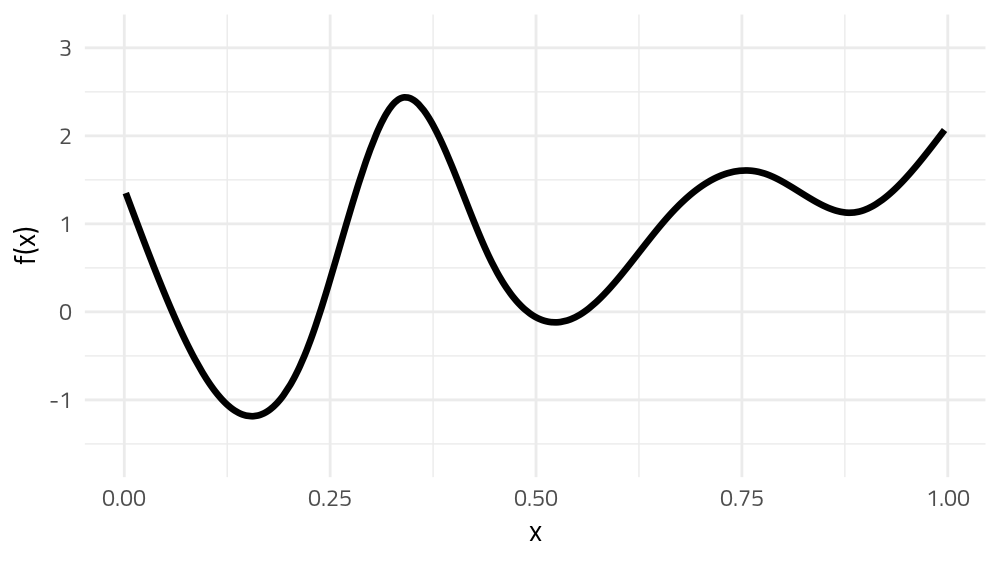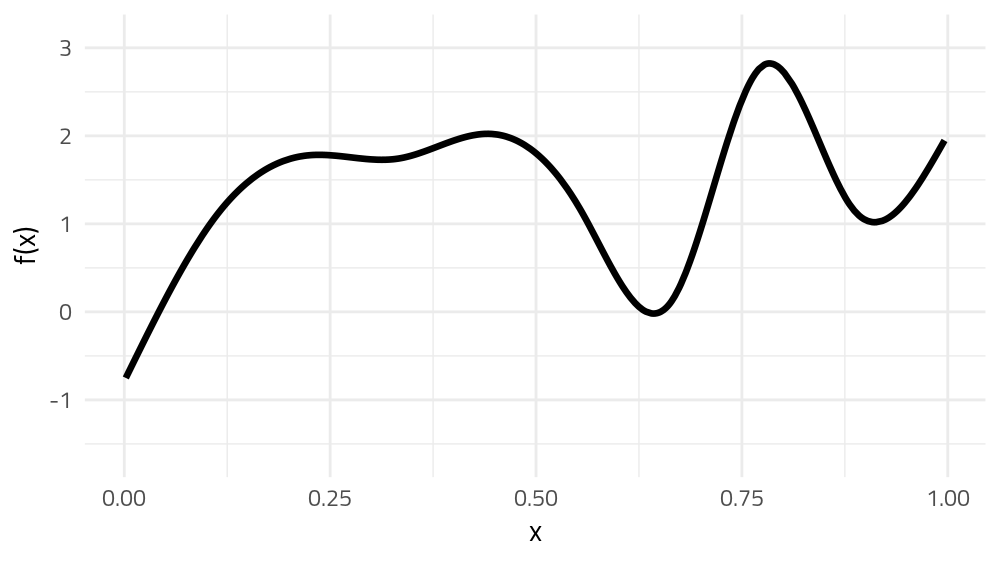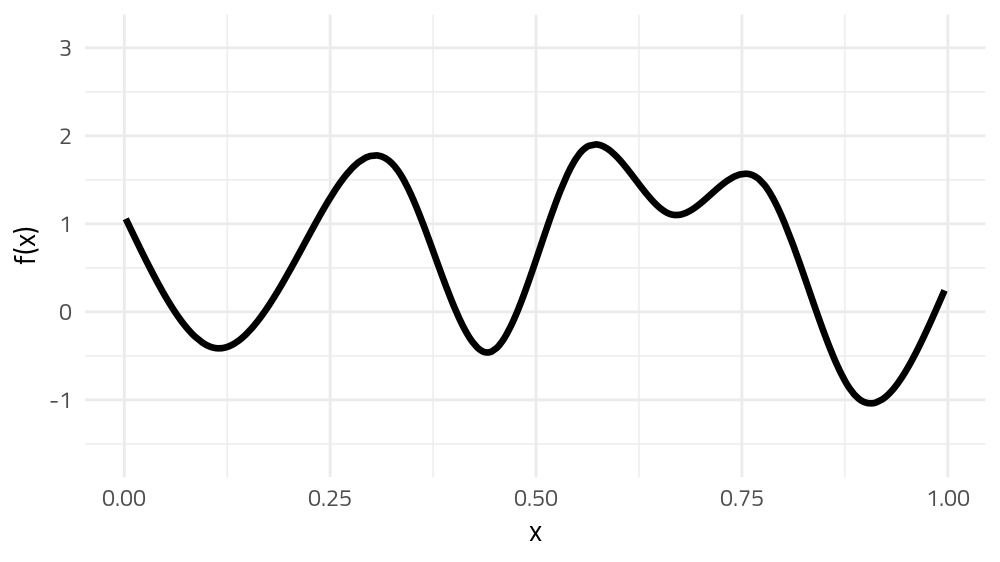
GAMs use splines to represent the non-linear relationships between covariates, here x, and the response variable on the y axis.

Splines formed from basis functions

Splines are built up from basis functions

Here I'm showing a cubic regression spline basis with 10 knots/functions

We weight each basis function to get a spline. Here all the basisi functions have the same weight so they would fit a horizontal line

Weight basis functions → spline

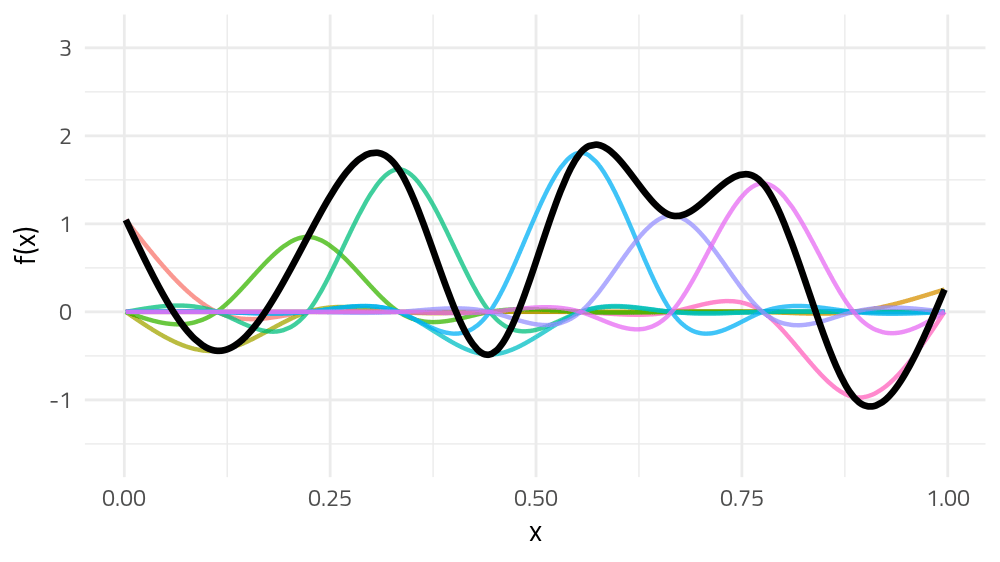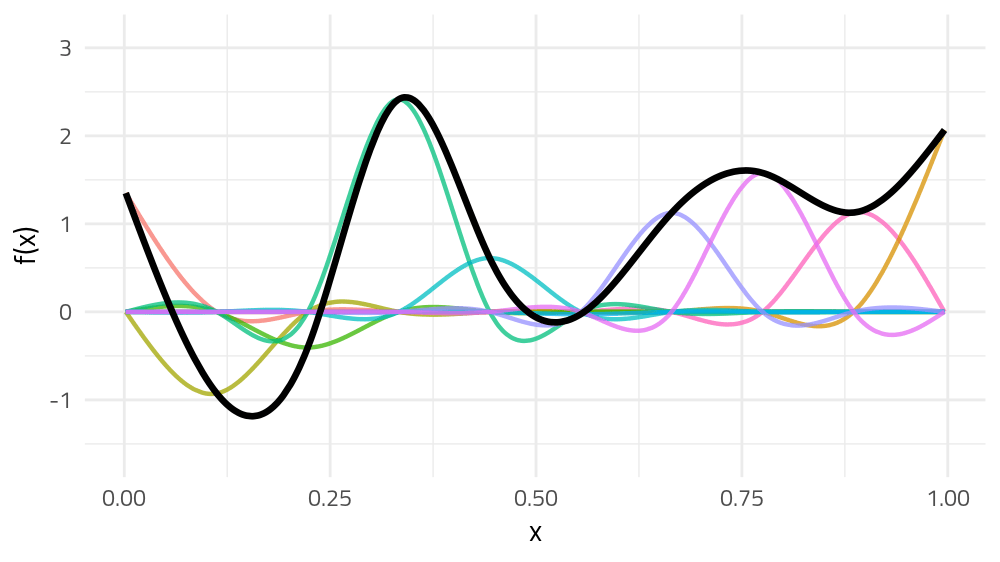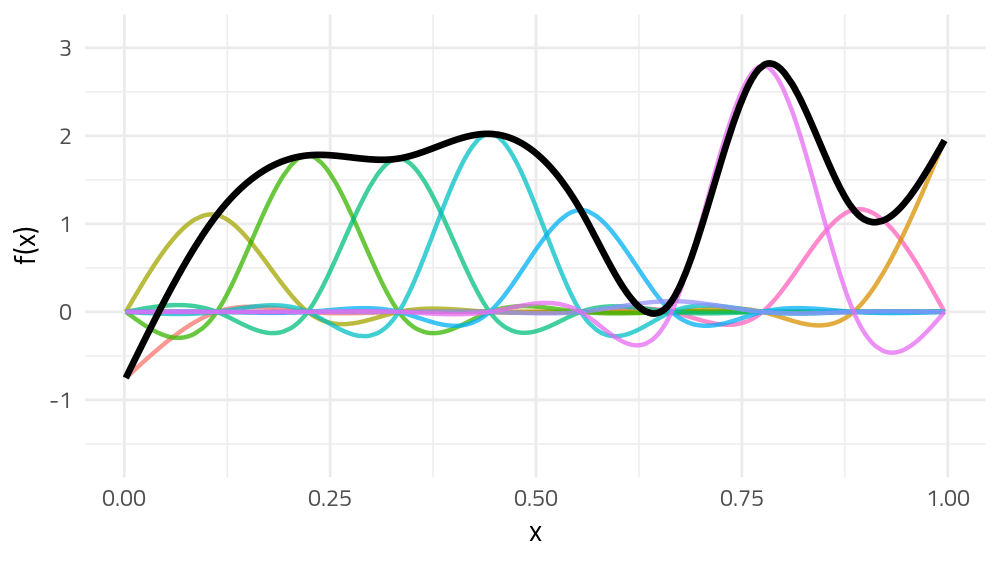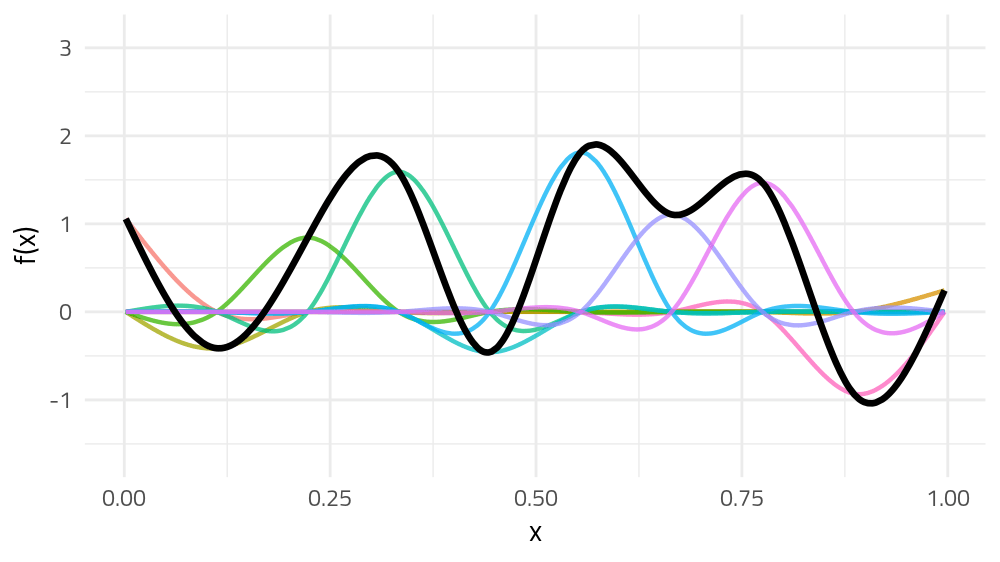
But if we choose different weights we get more wiggly spline

Each of the splines I showed you earlier are all generated from the same basis functions but using different weights

How do GAMs learn from data?

How does this help us learn from data?

Here I'm showing a simulated data set, where the data are drawn from the orange functions, with noise. We want to learn the orange function from the data

Choose weights to best fit data

Fitting a GAM involves finding the weights for the basis functions that produce a spline that fits the data best, subject to some constraints

Avoid overfitting our sample

Use a wiggliness penalty — avoid fitting too wibbly wobbly models

Outputs

  • Developing methodological approaches

  • Developing packages to enable model-fitting by other scientists

  • Training

Simpson (2018) Frontiers in Ecology & Evolution

doi: 10/gfrc4p

Pedersen et al (2019) PeerJ

doi: 10/c6wz

Trends in water quality data

Memes are cool

Why statistics?

  • Estimate effect size

  • Estimate variance

  • Make predictions from a model

Why statistics?

  • Estimate effect size

  • Estimate variance

  • Make predictions from a model

Stats are cool™

Badly explained stats

Stats profs be like

Badly explained stats

Stats profs be like

Students be like

Badly explained stats

GAMs

  1. Conditional distribution

  2.  

  3.  

yi∼EF(μi,Θ)

Badly explained stats

GAMs

  1. Conditional distribution

  2. Link function

  3.  

g(E(yi))=g(μi)=ηi

Badly explained stats

GAMs

  1. Conditional distribution

  2. Link function

  3. Linear predictor

η=β0+∑j=1pfj(xj)

Badly explained stats

GAMs

  1. Conditional distribution

  2. Link function

  3. Linear predictor

Homework: read chapter on GAMs and do ex. 1–20

Let's skip the theory and see the applications!

Master Agreement on Apportionment

  • 12 rivers in AB, SK, MB

  • Apportionment of inter-provincial river water

  • Water quality objectives

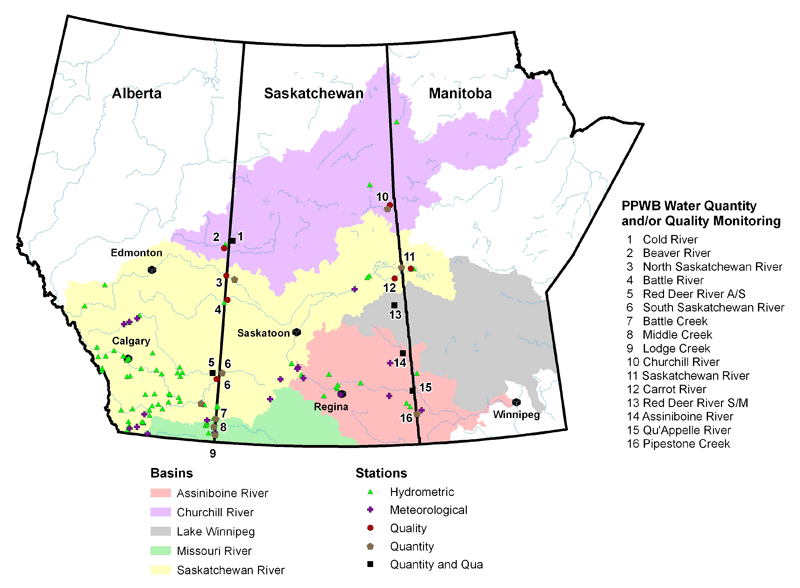
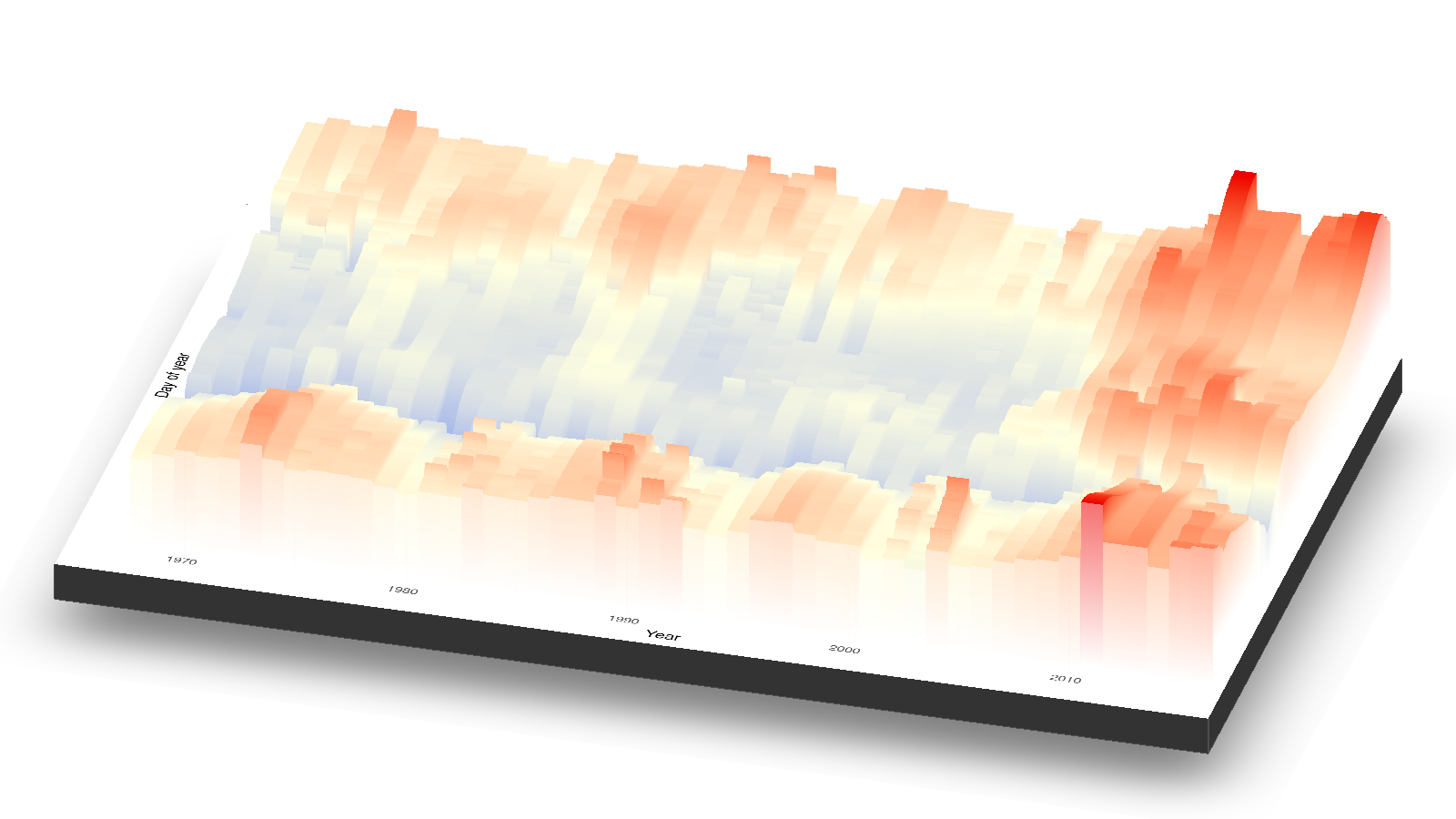
Sulphate in the Assiniboine River

Sulphate in the Assiniboine River

Sulphate ([SO4]) in Assiniboine River near Shellmouth

  • No significant increases over the years

  • Keep [SO4] < 299 mg L-1

The data

The seasonal Mann-Kendall test

  • Test statistic used for the detection of a trend in a time series

  • Commonly used for water quality assessment (Hirsch et al. 1982)

  • Used by the Prairie Provinces Water Board — responsible for MAA

  • Assumes that the trend is monotonic

Hirsch, R.M., Slack, J.R. and Smith, R.A. (1982), Techniques for trend assessment for monthly water quality data, Water Resources Research 18, 107–121.

GAMs should provide a more robust approach to trend detection

Model structure I

Create a model with year, seasonal, and flow effects

Model structure I

Create a model with year, seasonal, and flow effects

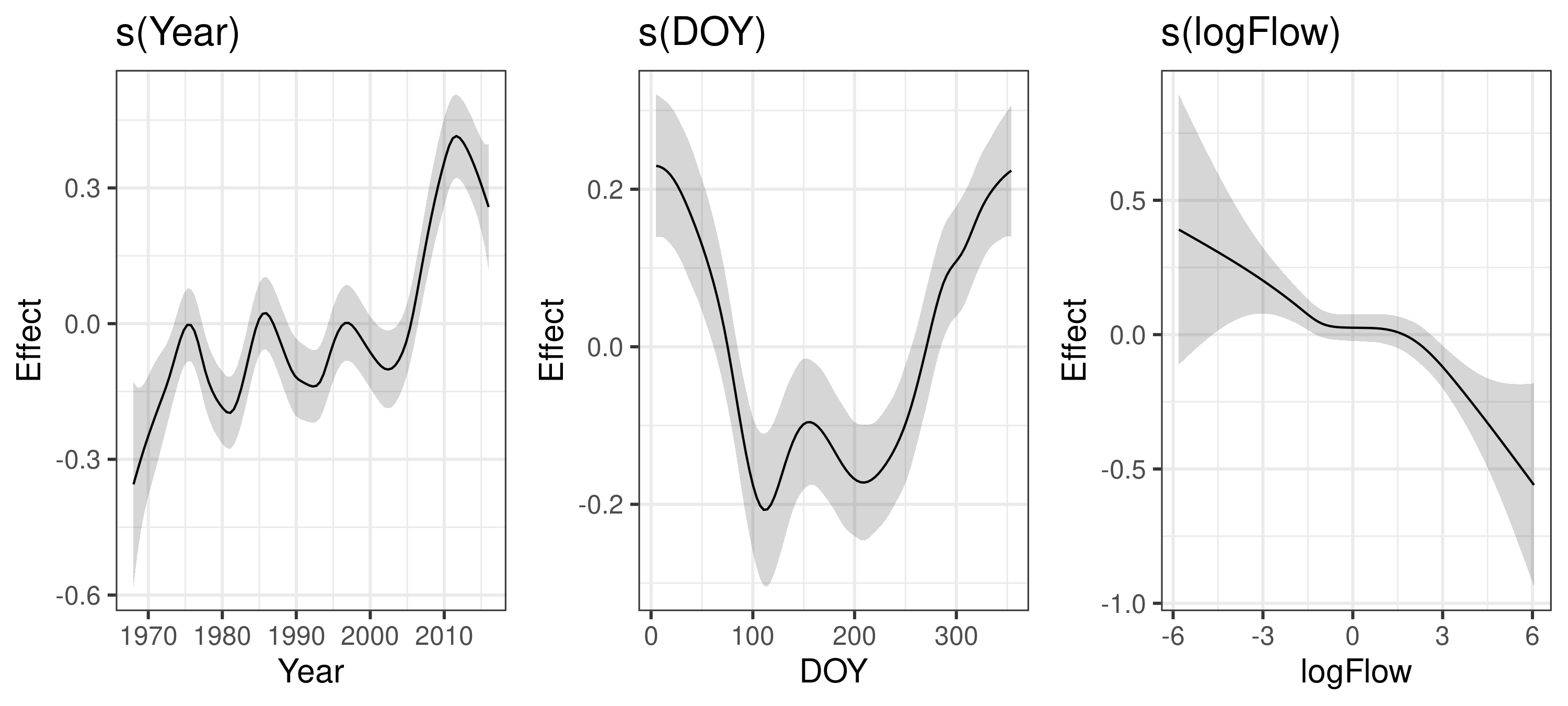
Model structure II

Add interactions between terms

Model structure II

Add interactions between terms

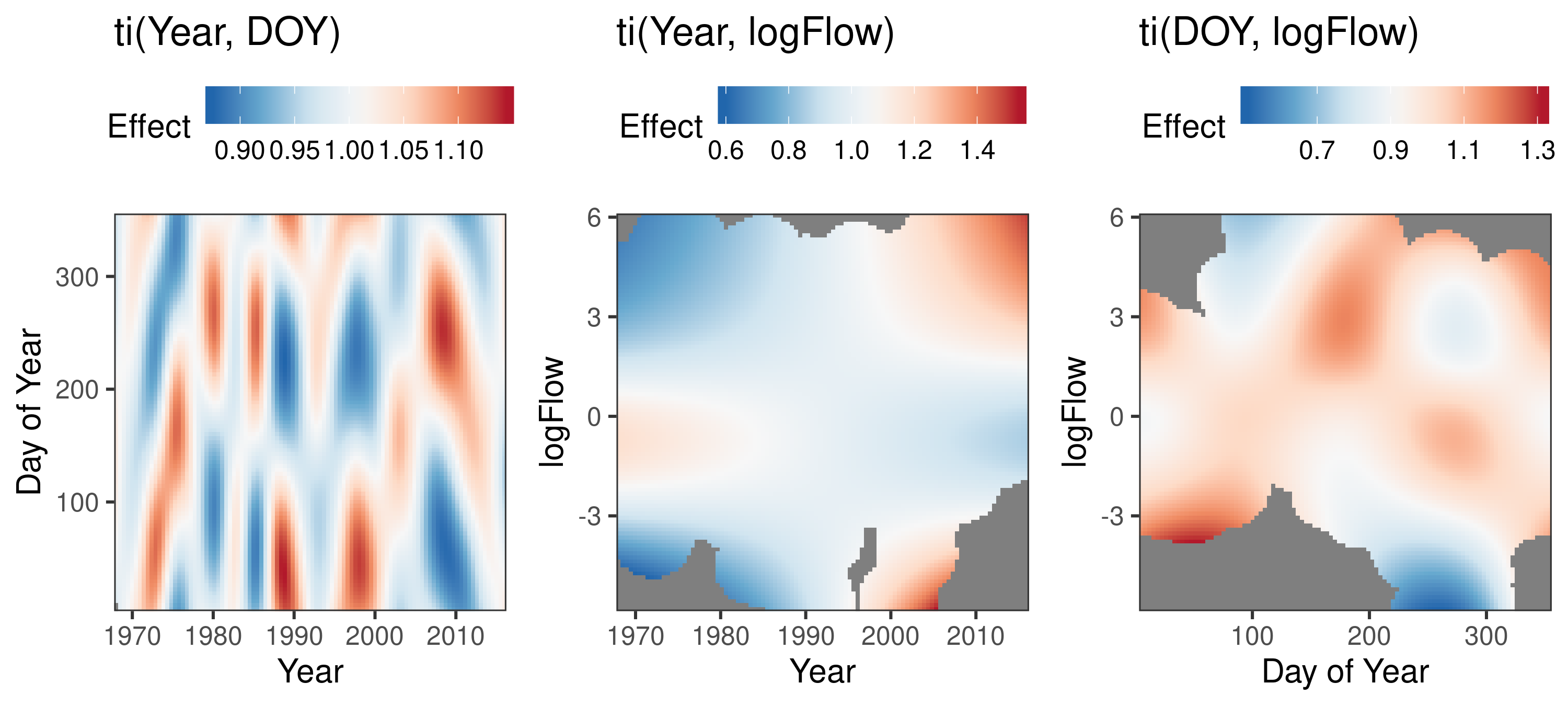
How seasonal patterns change over the years, How the effect of flow changes over the years (e.g. FX of dilution in seasons of high/low pollution), How the effect of flow changes over the seasons (e.g. FX of dilution in years of high/low pollution)

Using the model

  1. Estimate E([SO4]) over time

  2. Estimate probability [SO4] exceeds the guideline (299 mg L-1) over time

  3. Identify years of significant increase in [SO4]

Expected [SO4] over time


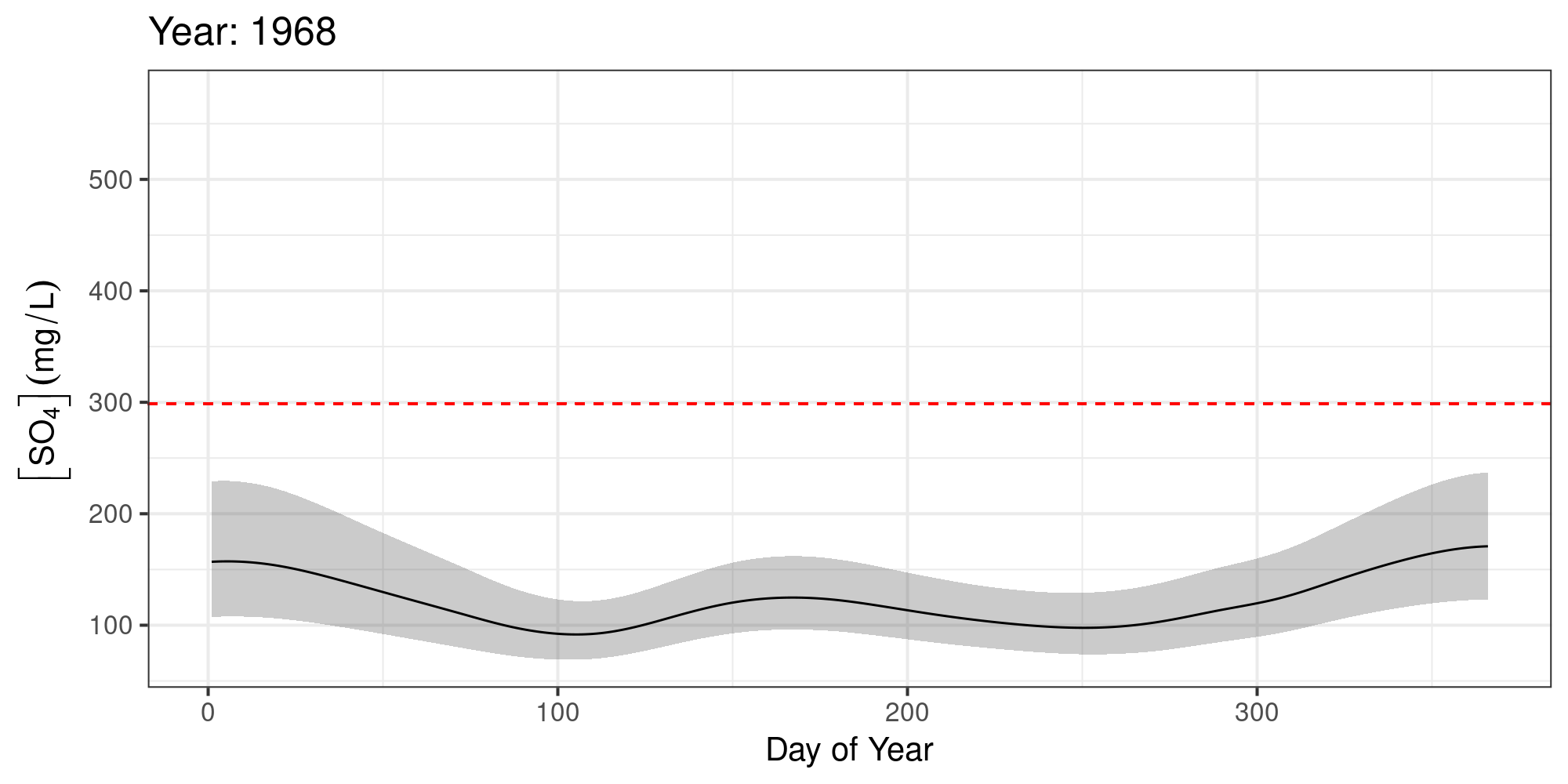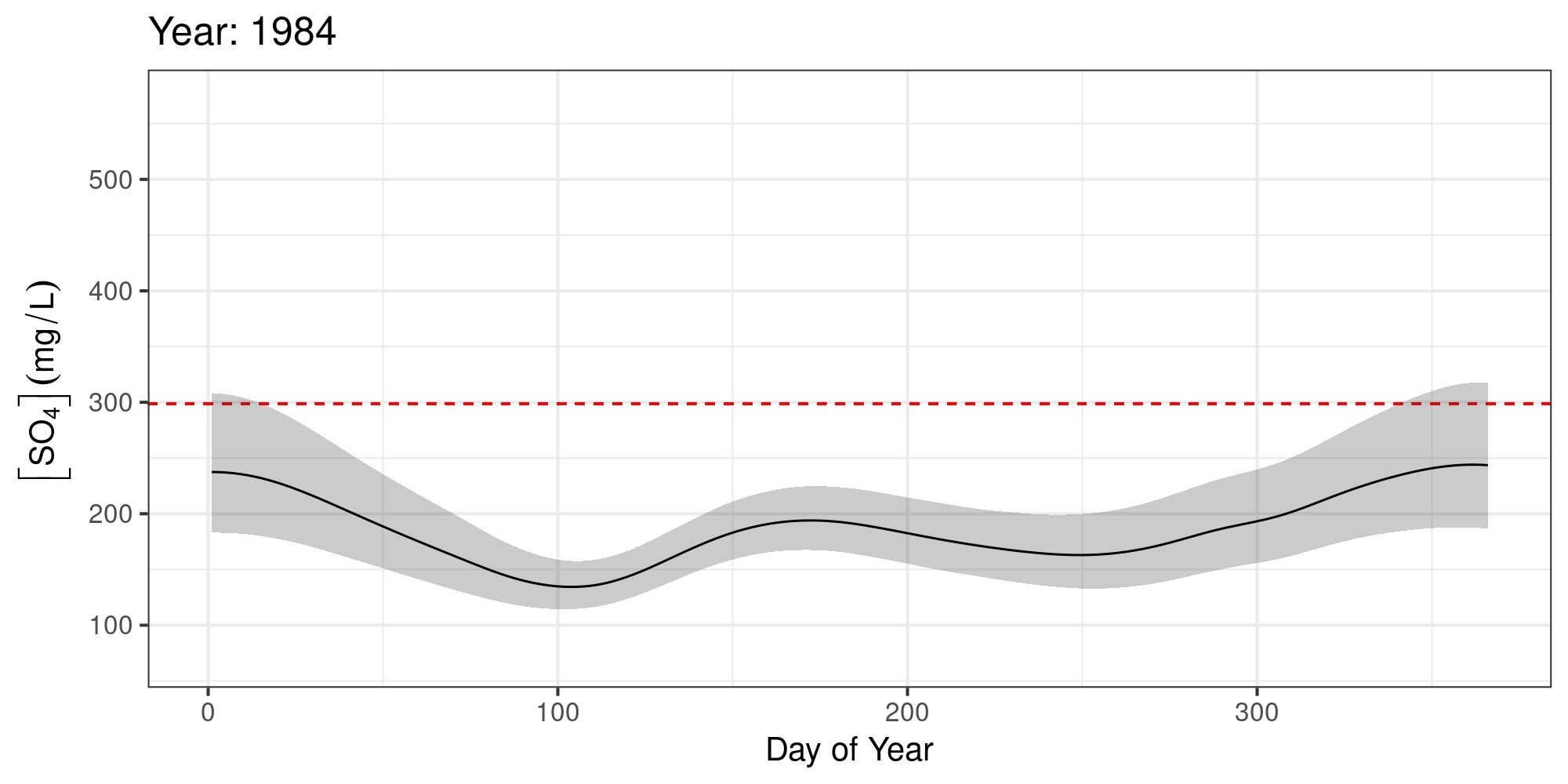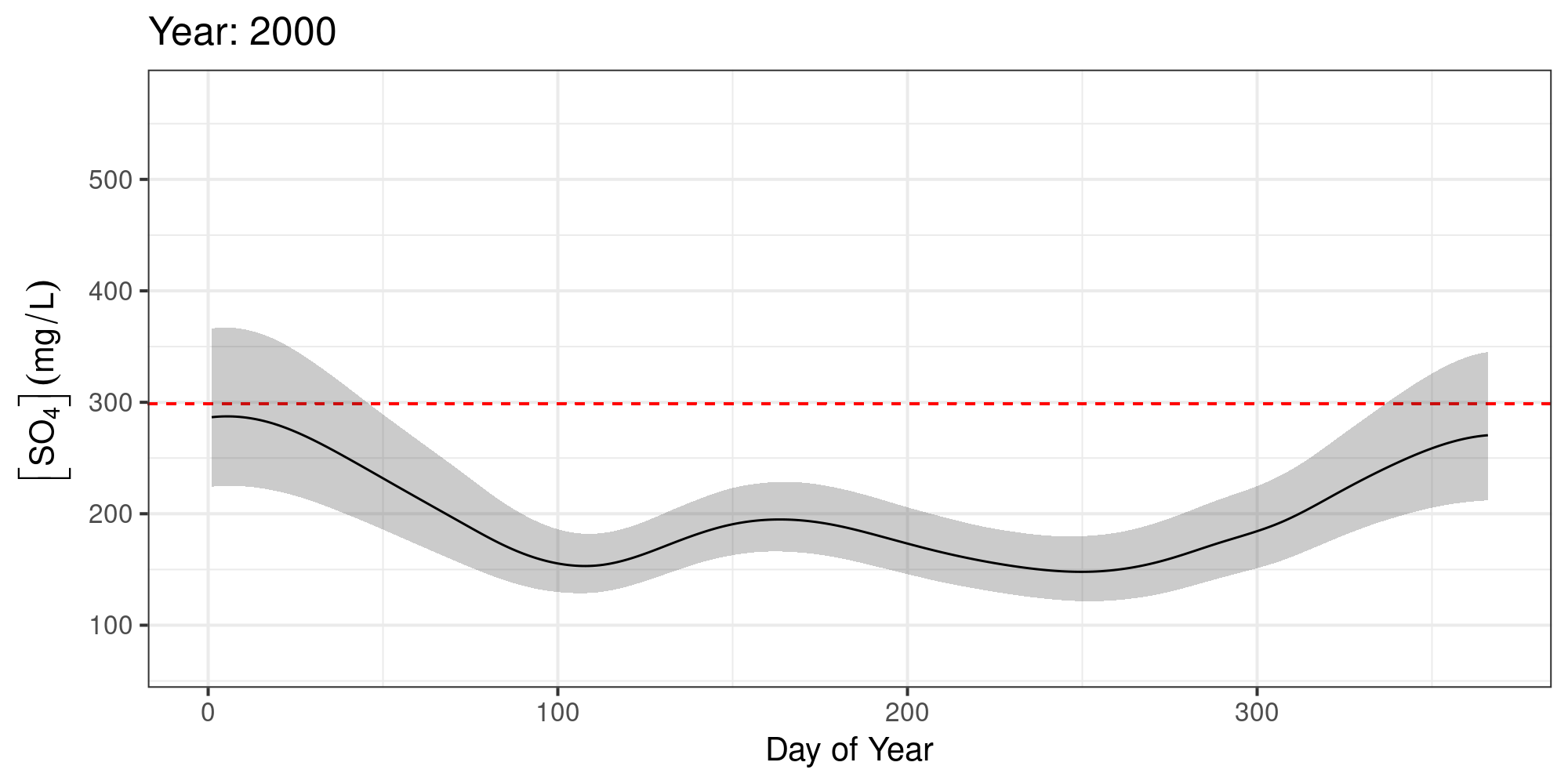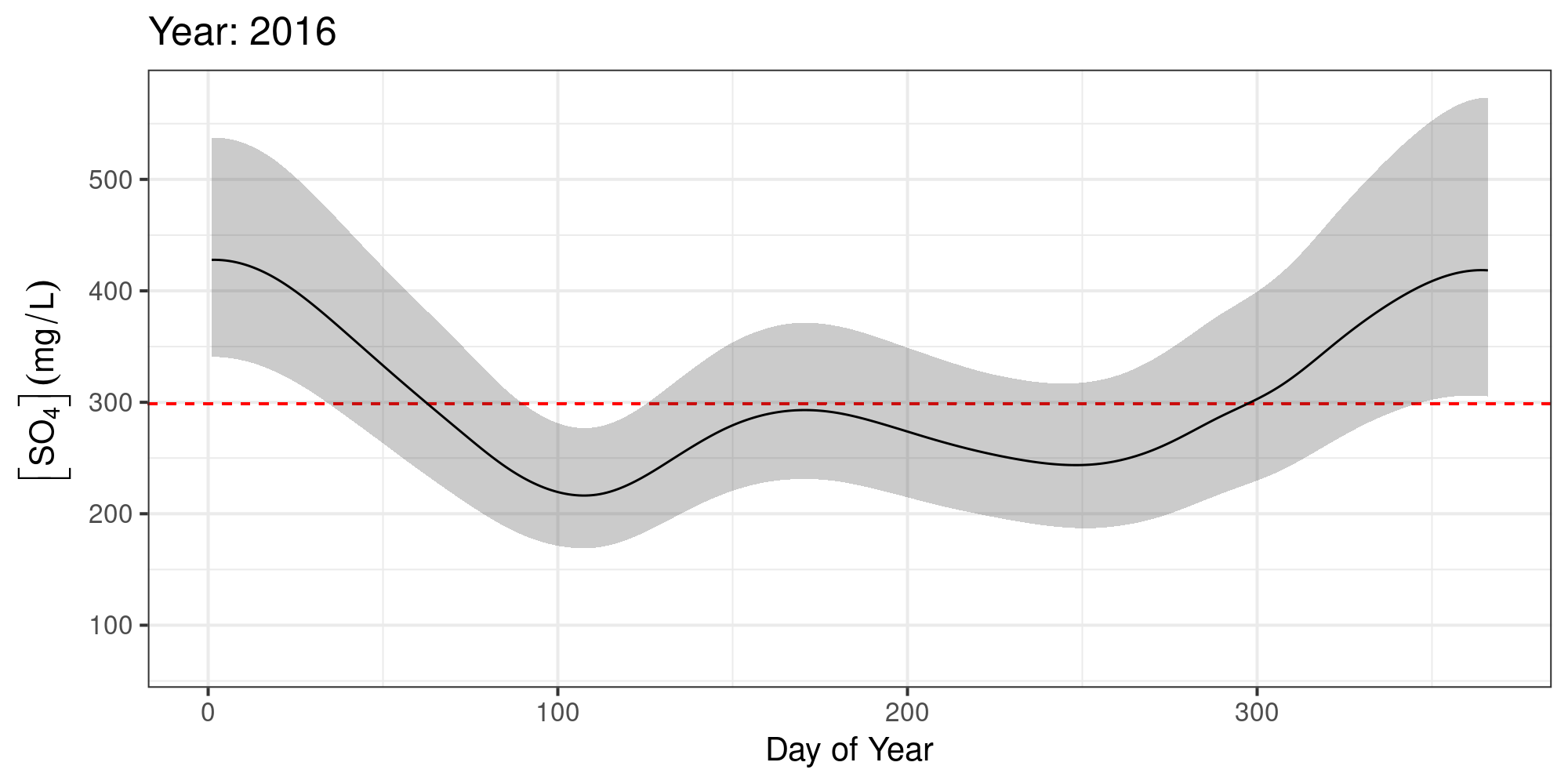
Expected [SO4] given log(Flow)

P( [SO4] >299 mg L-1 ) given log(Flow)

Instantaneous rate of change


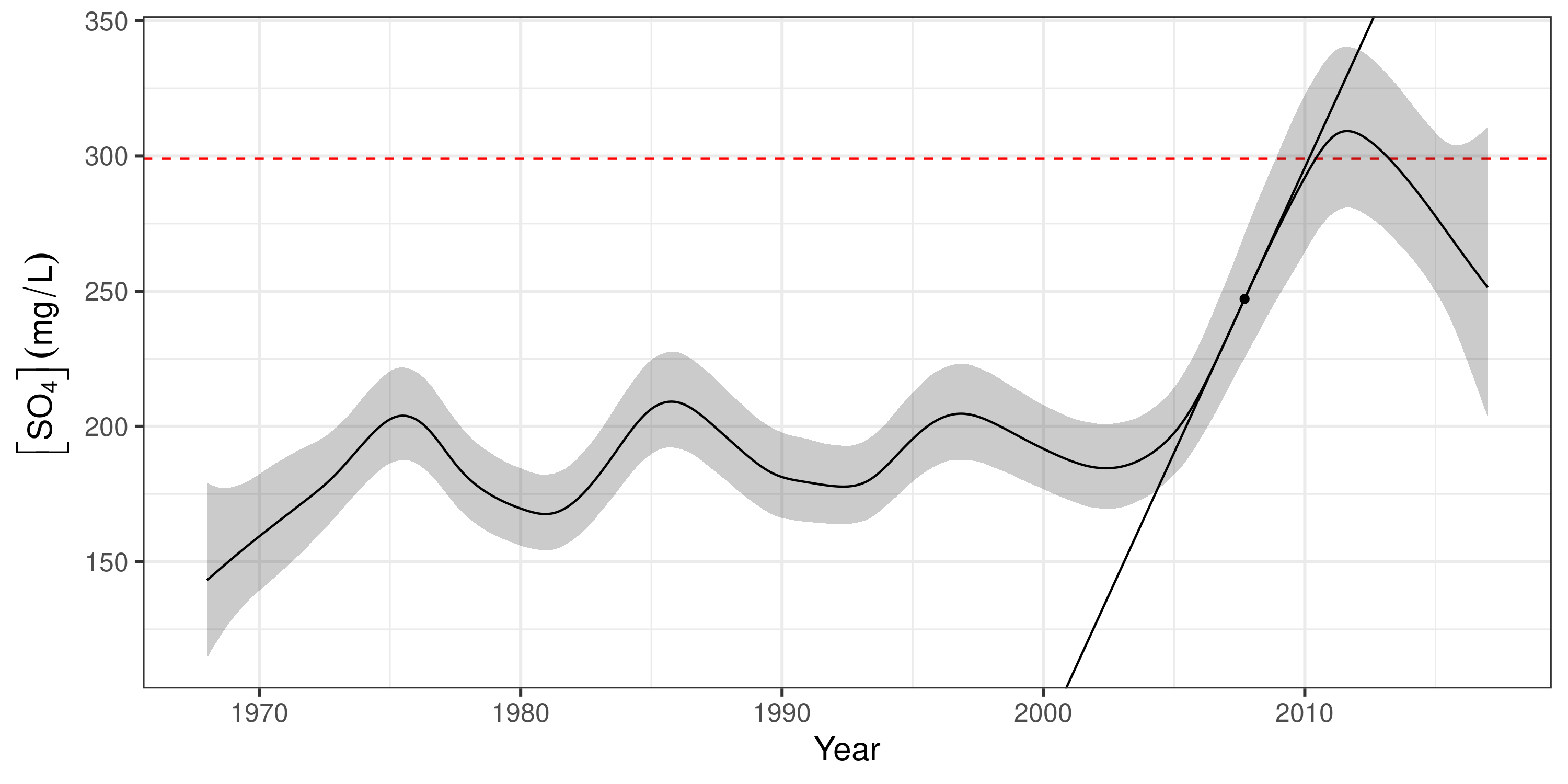
Identify periods of change


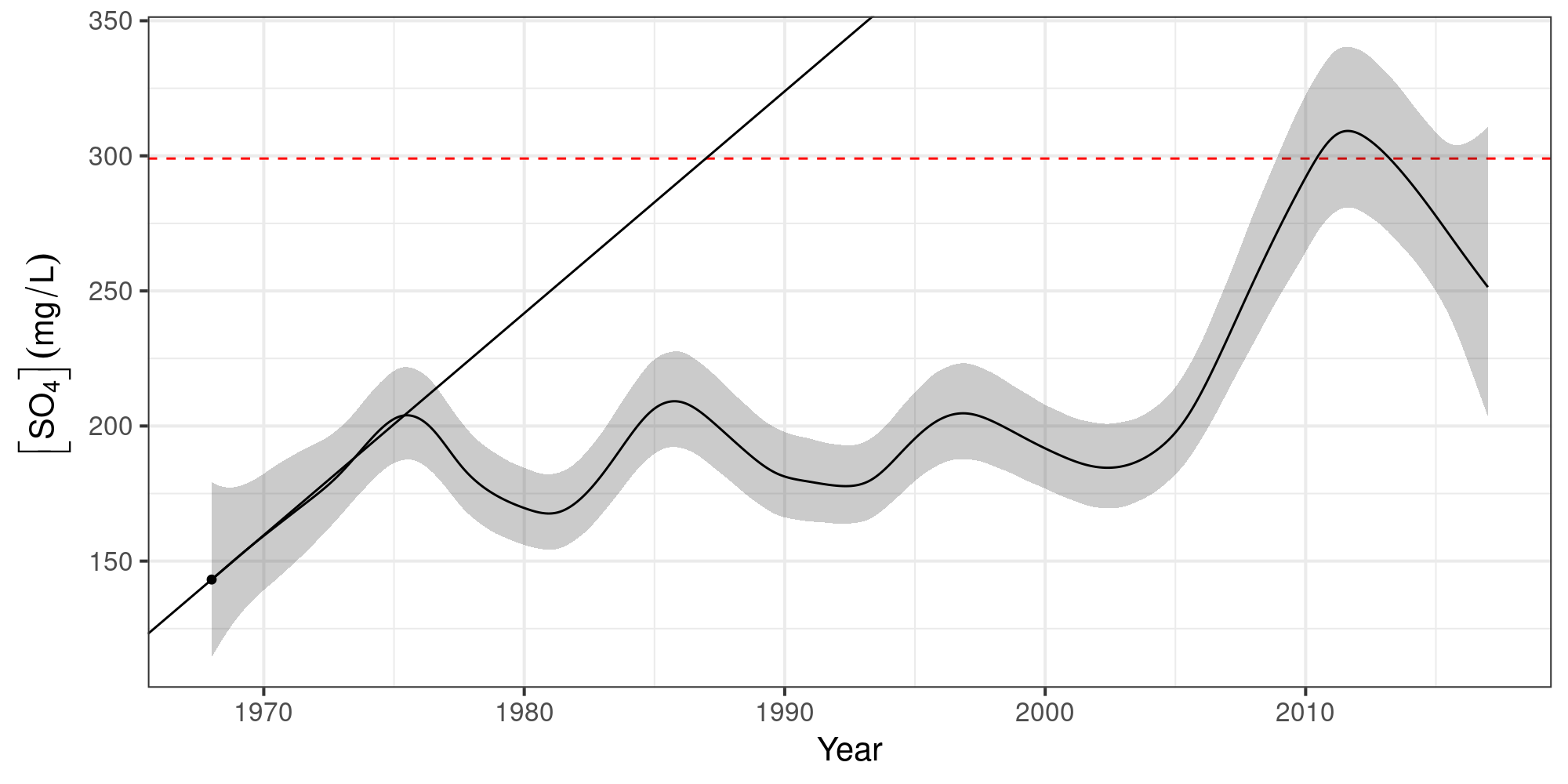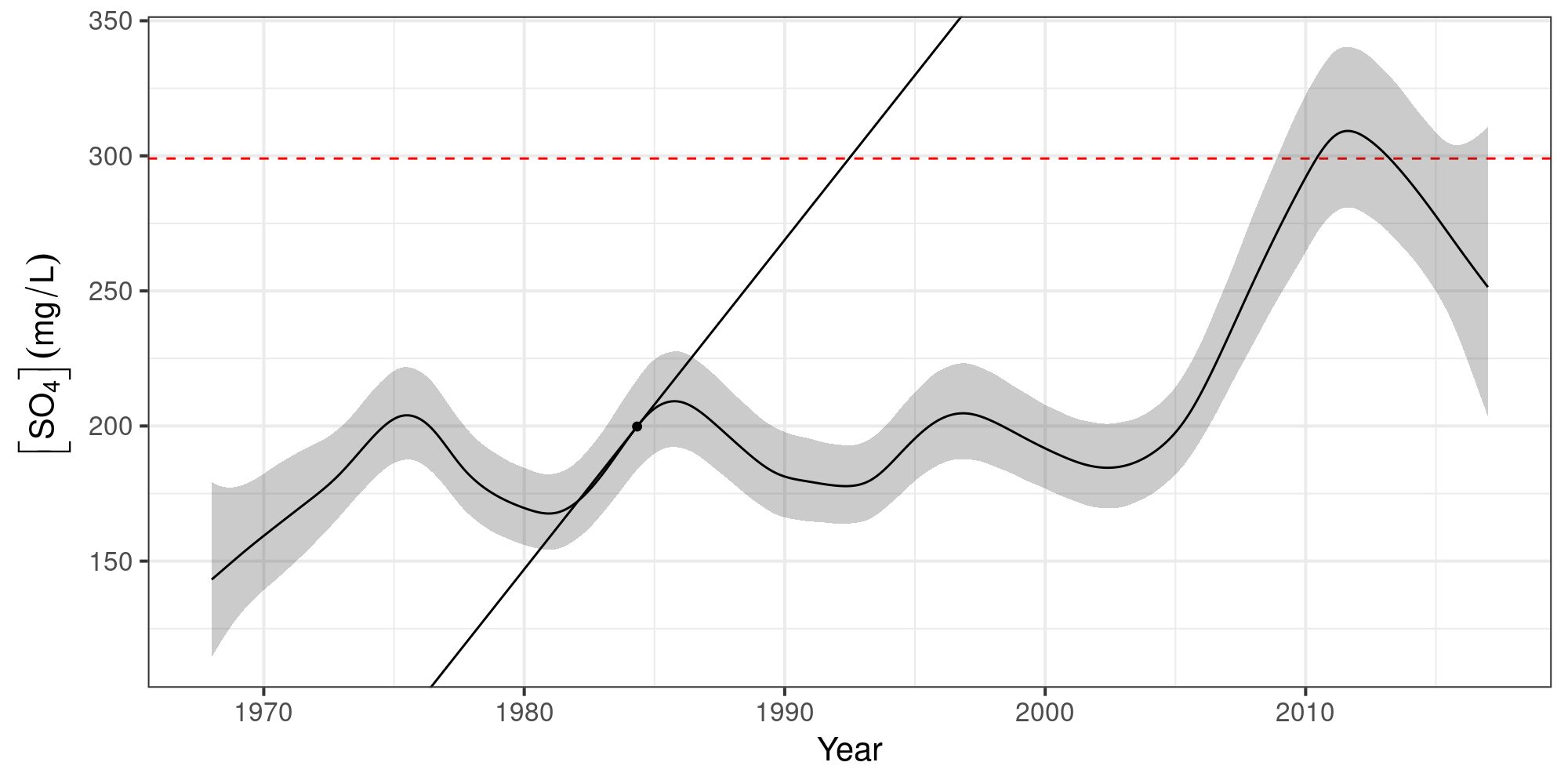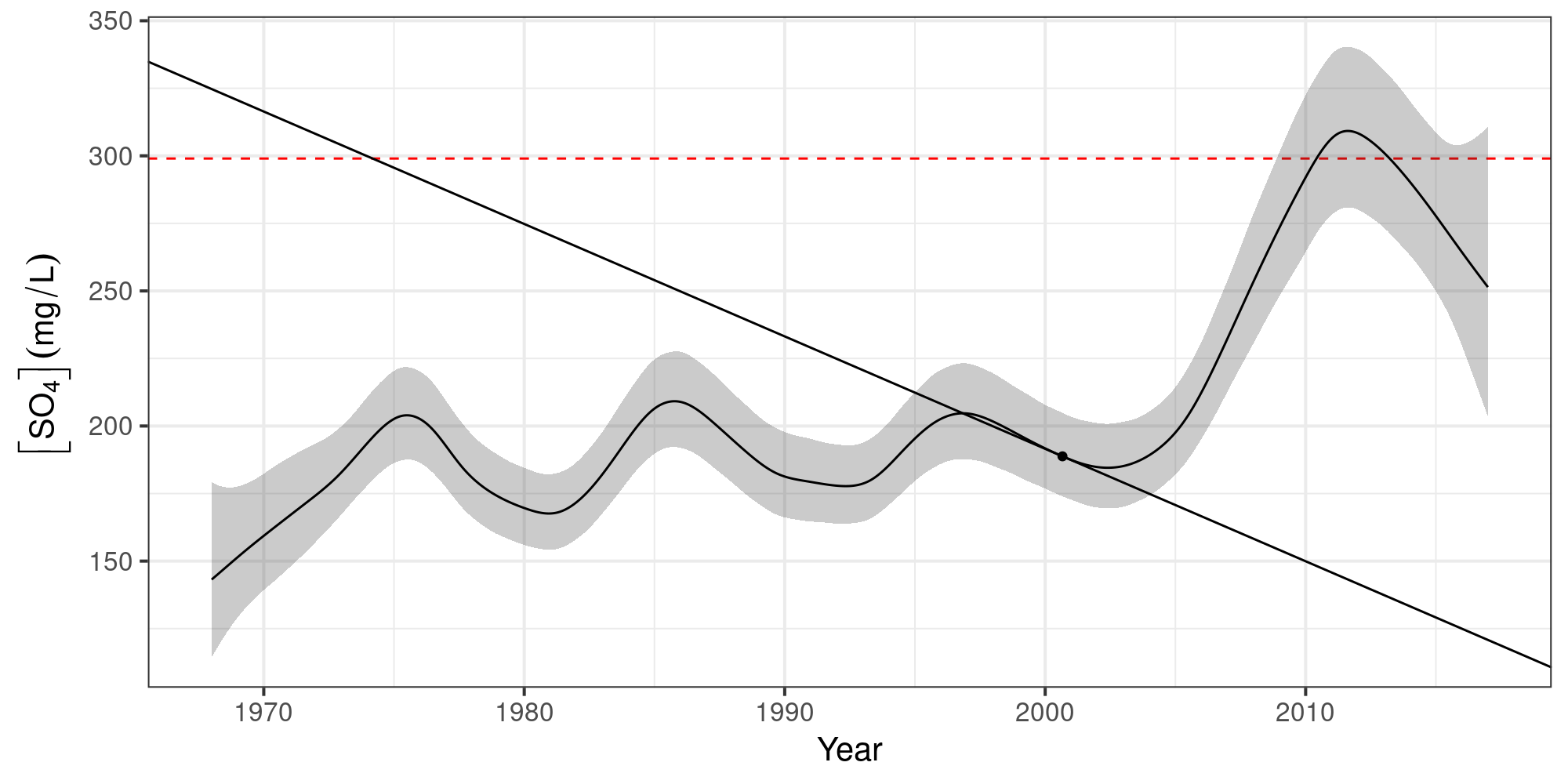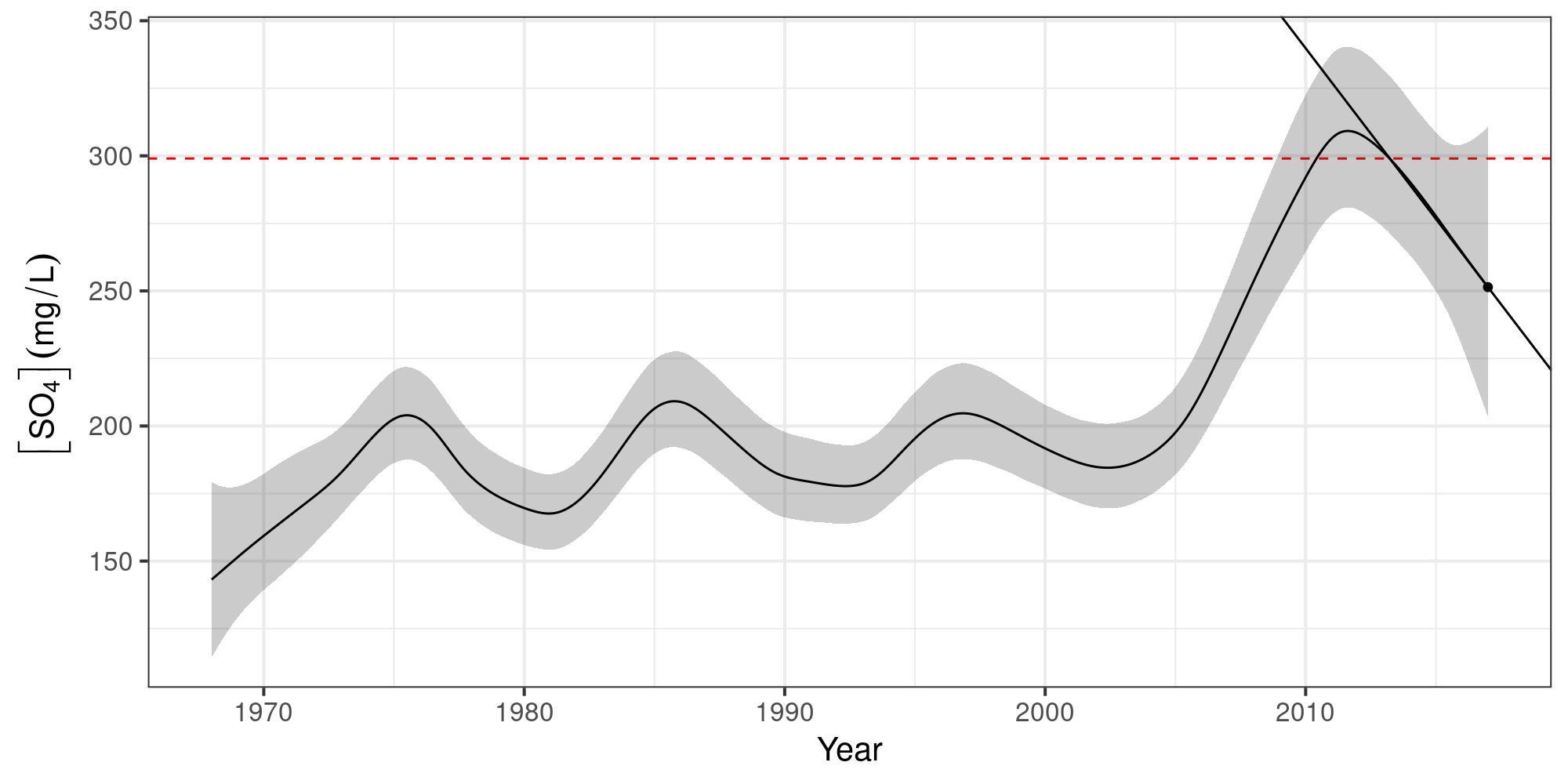
using α = 0.05
as a guide…

Identify periods of significant change


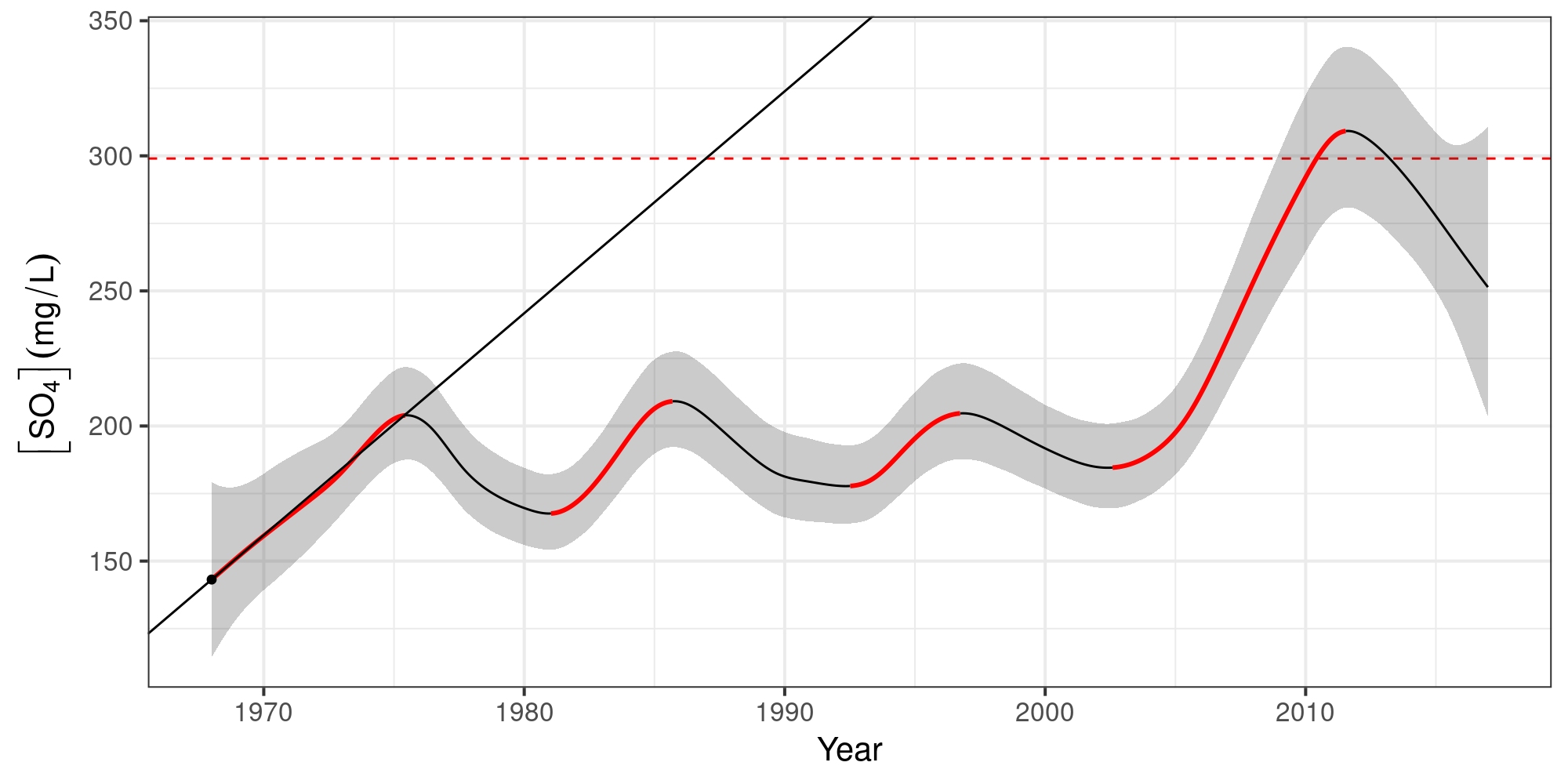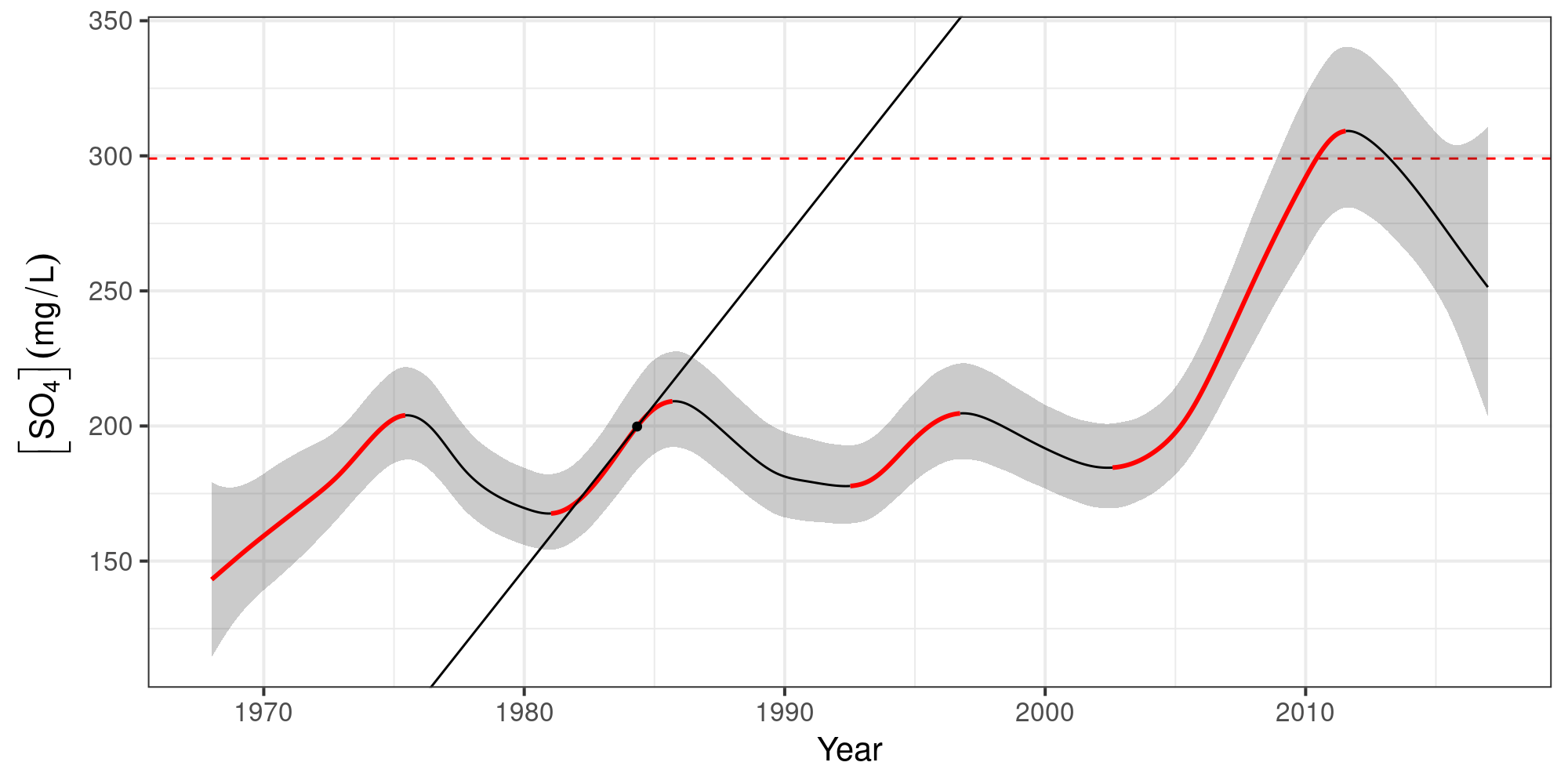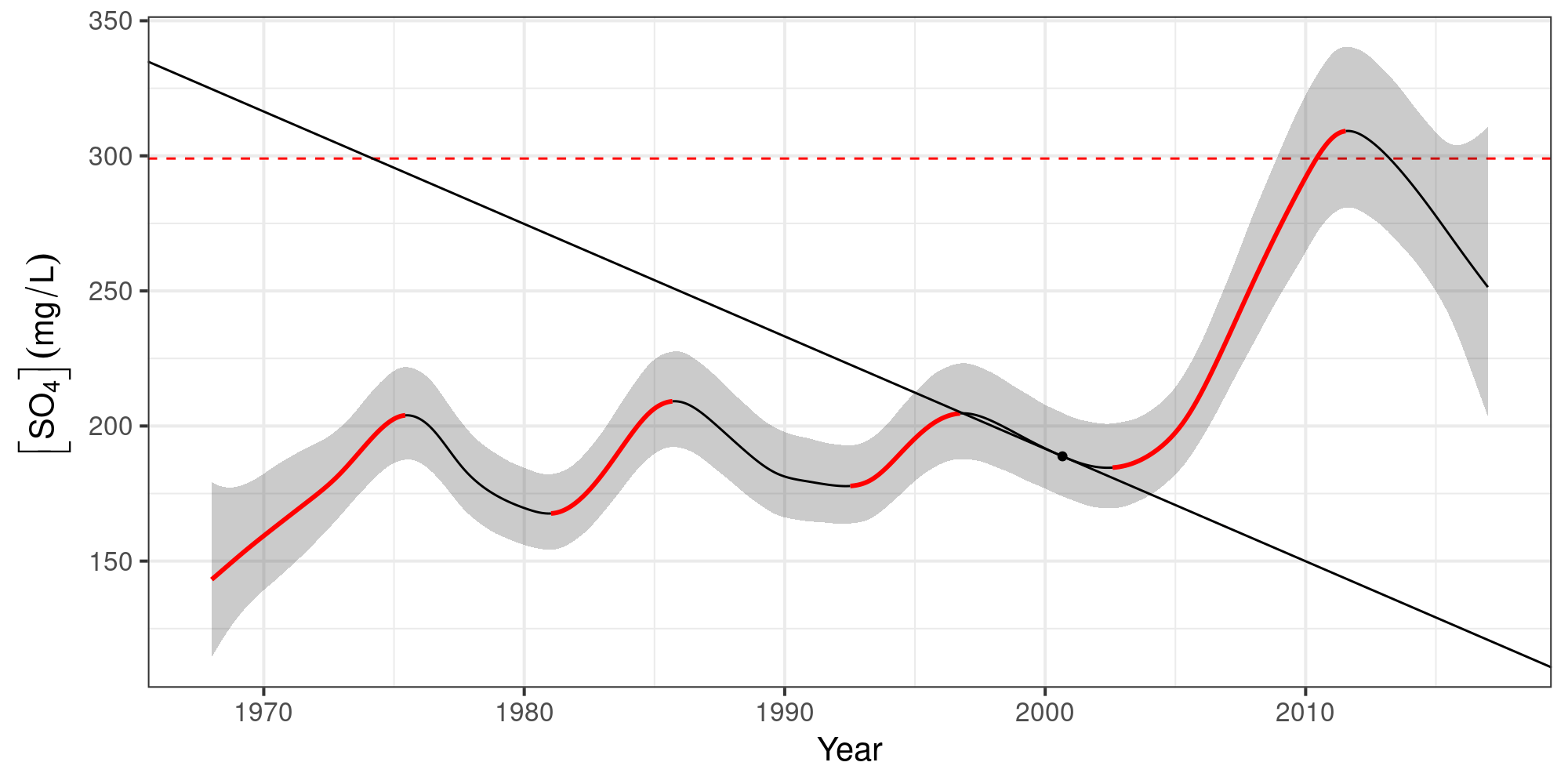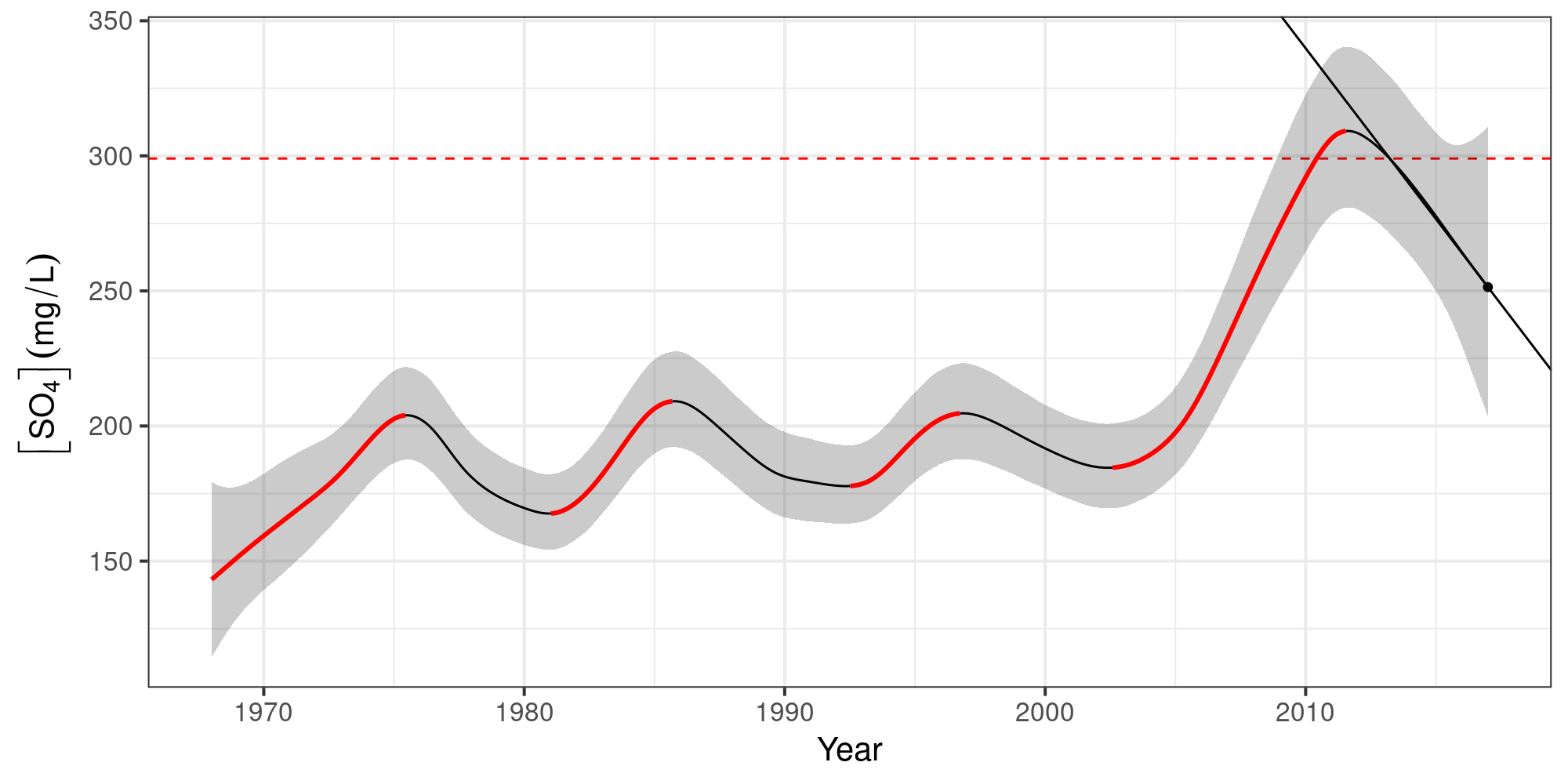
Conclusions

Using the model we can show that:

  1. The expected value of [SO4] was often > 299 mg L-1 — esp. after 2010

  2. The probability that [SO4] exceeded 299 mg L-1 was often high — esp. after 2010

  3. [SO4] increased markedly post 2008 — failure of the water quality objectives


[SO4] in the Assiniboine River should be monitored more closely

Saskatchewan's changing climate

Saskatchewan's
temperature

  • Adjusted and Homogenized Canadian Climate Data (AHCCD)

  • Monthly mean temperature

  • 36 climate stations

  • Variables

    • Year
    • Month
    • Latitude
    • Longitude
    • Climate Station

  • 36693 observations

~ 36 stations ranging from Uranium City in the Taiga Shield to Poplar River near the Canadian-US border

Random effect allows the model to account for the variance between locations due to any systematic/random error

There 36 693 observations

Daily temperature data are available, and models have been run for these, but we decided to use monthly temperature because there were less than 37 thousand observations vs the 1.1 million

Mention map

yes… moar GAMs…

To show changing trends, I used HGAM…

After Gavin’s and Stefano’s presentations, expect one of the following thoughts on GAMs.

At the very simplest, GAMs better model wiggly data and show trends more accurately than linear models would

Hierarchical GAMs

Don’t freak out before I get the chance to present on why I’m really here

HGAMs are a lot simpler than you may expect

Only difference is data can be grouped, and trends can vary between the groups

Hierarchical GAMs

  • HGAMs are similar to GAMs

  • Instead of one model per time series, model all time series at once

  • Smooths can vary between time series

  • Can determine

    • common trend over all stations

    • unique trend for each station

Quick heads up

The Stavrinauts made me add this…

Why a hierarchical GAM?

Not to bore with stats jargon

Many studies of Canadian temperature & climate data

Individual linear models for each climate station

Have to compare all the models post hoc

We know temperature not changing linearly

HGAMs allow us to model wiggly curves and account for spatial trends

HGAMs allow us to model wiggly curves to the data and account for location differences, all in one model

Effects of time

Break down components of the model

Left: average seasonal trend across all stations, summers much warmer than winters

Effects of time

Difference is 30-40 degrees

Middle: temperature change throughout the years

Fewer temperature stations in the beginning, hence the large Cis

Temperature has become more variable between years

Right: while left shows average trends, the right plot shows how seasonal trends have changed by year

Seasonal temperature changes over time

Three main cities in Saskatchewan for last 118 years

Temperatures are increasing throughout the seasons, but the winters are more drastic

Effect of space

  • Northern SK is colder than southern SK

First thing to notice is that north SK is colder than south SK

Effect of space

  • Northern SK is colder than southern SK

  • Difference is about 9℃

  • Fewer stations in northern SK

  • Need to use the model to extrapolate between stations

9 degrees difference

Fewer stations in north; therefore, use model to extrapolate for all possible

Space & time

  • 2018 modelled temperature

  • Spatial pattern changes throughout the year

  • Greater temperature variability in northern SK

How spatial trends change throughout the year

North SK has these two vertical bands that are warmer in the summer and colder in the winter than the adjacent area

South SK is not as variable and remains even throughout the year

Effects of time

Refresher, these plots show the global/average trend, but we also want to know how individual stations vary around these average trends

Station effects

First plot shows how locations vary within years

Some have warmer winters and cooler summers than average

Some are the inverse. Most stay around the average

Second plot: how locations vary throughout the years

Again, most stay around the average. But some have increased

Two weird ones that have cooled and are now closer to the average

Conclusions

  • HGAMs are useful for modelling wiggly data from many climate stations

  • Temperatures have significantly increased across Saskatchewan since the 1880s

  • This change is more clearly seen in the winter months

  • Seasonal trends vary spatially and temporally

  • Significant variation in the trends at each climate station

Climate change affecting lake temperatures?

Data: Woolway et al (2019) Climate Change 155, 81–94 doi: 10/c7z9

Why worry about minimum temperatures?

Why worry about minimum temperatures?

Annual minimum temperature is a strong control on many in-lake processes (eg Hampton et al 2017)

Extreme events can have long-lasting effects on lake ecology — mild winter in Europe 2006–7 (eg Straile et al 2010)

Reduction in habitat or refugia for cold-adapted species

  • Arctic charr (Salvelinus alpinus)
  • Opossum shrimp (Mysis salemaai)

Hampton et al (2017). Ecology under lake ice. Ecology Letters 20, 98–111. doi: 10/f3tpzh

Straile et al (2010). Effects of a half a millennium winter on a deep lake — a shape of things to come? Global Change Biology 16, 2844–2856. doi: 10/bx6t4d

Multiple time series → HGAM

central limit theorem

Central limit theorem shows us that the Gaussian or normal distribution is the sampling distribution for many sample statistics, including sample means, as samples sizes become large

Central limit theorem underlies much of the theory that justifies much of the statistics you learn about in your statistics courses, and supports the use of the Gaussian or normal distribution

Annual minimum temperature

block minima

Fisher–Tippett–Gnedenko theorem

The maximum of a sample of iid random variables after proper renormalization can only converge in distribution to one of three possible distributions; the Gumbel distribution, the Fréchet distribution, or the Weibull distribution.

Source: Wikimedia Commons

Source: ral.ucar.edu

Source: Wikimedia Commons

block minima…?

highly technical fix

Negate the minima

plus some jiggery-pokery after model fitting

three distributions — WTF

Generalised extreme value distribution

In 1978 Daniel McFadden demonstrated the common functional form for all three distributions — the GEVD

G(y)=exp⁡{−[1+ξ(y−μσ)]+−1/ξ}

Three parameters to estimate

  • location μ,
  • scale σ, and
  • shape ξ

Three distributions

  • Gumbel distribution when ξ = 0,
  • Fréchet distribution when ξ > 0, and
  • Weibull distribution when ξ < 0

Fit HGAMLSS using GEV for response

HGAMLSS…?

Model μ, σ, ξ with smooths of Year

Estimated smooths

 

Summary

  • Lake minimum surface water temperatures have increased by on the order of 1–3 degrees over the last 60 years

  • Evidence that the distribution of annual minima has changed in many lakes — implications for future extreme events which have long-term knock-on effects

  • HGAMLSS with the GEV distribution are a good way of modelling common trends in environmental extremes

Acknowledgements

Funding

Data

  • Prairie Provinces Water Board — Dr. Joanne Sketchell
  • Environment and Climate Change Canada & Government of Canada
  • Iestyn Woolway and colleagues for archiving the lake surface water data

Slides

We meet today on Treaty 4 lands, the territories of the Cree, Saulteaux (SOH-toh), Dakota, Lakota, Nakoda, and the homeland of the Métis Nation.

Today, these lands continue to be the shared territory of many diverse peoples.

Paused

Help

Keyboard shortcuts

↑, ←, Pg Up, k Go to previous slide
↓, →, Pg Dn, Space, j Go to next slide
Home Go to first slide
End Go to last slide
Number + Return Go to specific slide
b / m / f Toggle blackout / mirrored / fullscreen mode
c Clone slideshow
p Toggle presenter mode
t Restart the presentation timer
?, h Toggle this help
Esc Back to slideshow