Logistics

Slides

Slide Deck: bit.ly/adv-vegan Sources: github.com/gavinsimpson/advanced-vegan-webinar-july-2020

Direct download a ZIP of everything: bit.ly/adv-vegan-zip

Unpack the zip & remember where you put it

Q & A

Add questions to Google Doc: bit.ly/adv-vegan-qa

Recording

Livestream will be recorded — link will be emailed to you later today

Today's topics

• Constrained ordination
  • Canonical Correspondence Analysis
  • Redundancy Analysis
  • Partial constrained ordination
• Model Building
  • Model selection
• Permutation tests
• Restricted permutation tests
• PERMANOVA
• Diagnostics

Canonical Correspondence Analysis

CCA is the constrained form of CA; fitted using cca()

Two interfaces for specifying models

• basic; cca1 <- cca(X = varespec, Y = varechem)
• formula; cca1 <- cca(varespec ~ ., data = varechem)

RDA is the constrained form of PCA; fitted using rda()

Formula interface is the more powerful — recommended

Canonical Correspondence Analysis

cca1 <- cca(varespec ~ ., data = varechem)
cca1

## Call: cca(formula = varespec ~ N + P + K + Ca + Mg + S + Al + Fe + Mn +
## Zn + Mo + Baresoil + Humdepth + pH, data = varechem)
## 
##               Inertia Proportion Rank
## Total          2.0832     1.0000     
## Constrained    1.4415     0.6920   14
## Unconstrained  0.6417     0.3080    9
## Inertia is scaled Chi-square 
## 
## Eigenvalues for constrained axes:
##   CCA1   CCA2   CCA3   CCA4   CCA5   CCA6   CCA7   CCA8   CCA9  CCA10  CCA11 
## 0.4389 0.2918 0.1628 0.1421 0.1180 0.0890 0.0703 0.0584 0.0311 0.0133 0.0084 
##  CCA12  CCA13  CCA14 
## 0.0065 0.0062 0.0047 
## 
## Eigenvalues for unconstrained axes:
##     CA1     CA2     CA3     CA4     CA5     CA6     CA7     CA8     CA9 
## 0.19776 0.14193 0.10117 0.07079 0.05330 0.03330 0.01887 0.01510 0.00949

Redundancy Analysis

rda1 <- rda(varespec ~ ., data = varechem)
rda1

## Call: rda(formula = varespec ~ N + P + K + Ca + Mg + S + Al + Fe + Mn +
## Zn + Mo + Baresoil + Humdepth + pH, data = varechem)
## 
##                 Inertia Proportion Rank
## Total         1825.6594     1.0000     
## Constrained   1459.8891     0.7997   14
## Unconstrained  365.7704     0.2003    9
## Inertia is variance 
## 
## Eigenvalues for constrained axes:
##  RDA1  RDA2  RDA3  RDA4  RDA5  RDA6  RDA7  RDA8  RDA9 RDA10 RDA11 RDA12 RDA13 
## 820.1 399.3 102.6  47.6  26.8  24.0  19.1  10.2   4.4   2.3   1.5   0.9   0.7 
## RDA14 
##   0.3 
## 
## Eigenvalues for unconstrained axes:
##    PC1    PC2    PC3    PC4    PC5    PC6    PC7    PC8    PC9 
## 186.19  88.46  38.19  18.40  12.84  10.55   5.52   4.52   1.09

The cca.object

• Objects of class "cca" are complex with many components
• Entire class described in ?cca.object
• Depending on what analysis performed some components may be NULL
• Used for (C)CA, PCA, RDA, CAP (capscale()), and dbRDA (dbrda())

The cca.object

cca1 has a large number of components

• $call how the function was called
• $grand.total in (C)CA sum of rowsum
• $rowsum the row sums
• $colsum the column sums
• $tot.chi total inertia, sum of Eigenvalues
• $pCCA Conditioned (partial-ed out) components
• $CCA Constrained components
• $CA Unconstrained components
• $method Ordination method used
• $inertia Description of what inertia is

The cca.object

Depending on how one called cca() etc some of these components will be NULL

$pCCA is only filled in if a partial constrained ordination fitted

rda() returns objects with classes "rda" and "cca", but in most cases those objects work like those of class "cca"

The Eigenvalues and axis scores are now spread about the $CA and $CCA components (also $pCCA if a partial CCA)

Thankfully we can use extractor functions to get at such things

Eigenvalues

Use eigenvals() to extract Eigenvalues from a fitted ordination object

eigenvals(cca1)

##      CCA1      CCA2      CCA3      CCA4      CCA5      CCA6      CCA7      CCA8 
## 0.4388704 0.2917753 0.1628465 0.1421302 0.1179519 0.0890291 0.0702945 0.0583592 
##      CCA9     CCA10     CCA11     CCA12     CCA13     CCA14       CA1       CA2 
## 0.0311408 0.0132944 0.0083644 0.0065385 0.0061563 0.0047332 0.1977645 0.1419256 
##       CA3       CA4       CA5       CA6       CA7       CA8       CA9 
## 0.1011741 0.0707868 0.0533034 0.0332994 0.0188676 0.0151044 0.0094876

Example

• Fit a CCA model to the lichen pasture data. The model should include, N, P, and K only.
• Save the model in object mycca1
• How much variance is explained by this model?
• Extract the eigenvalues, how many constrained axes are there?

library("vegan")
data(varechem, varespec)

mycca1 <- cca(varespec ~ N + P + K, data = varechem)
mycca1

## Call: cca(formula = varespec ~ N + P + K, data = varechem)
## 
##               Inertia Proportion Rank
## Total          2.0832     1.0000     
## Constrained    0.4464     0.2143    3
## Unconstrained  1.6368     0.7857   20
## Inertia is scaled Chi-square 
## 
## Eigenvalues for constrained axes:
##    CCA1    CCA2    CCA3 
## 0.19309 0.16271 0.09060 
## 
## Eigenvalues for unconstrained axes:
##    CA1    CA2    CA3    CA4    CA5    CA6    CA7    CA8 
## 0.4495 0.2870 0.1877 0.1675 0.1280 0.1050 0.0750 0.0629 
## (Showing 8 of 20 unconstrained eigenvalues)

ev <- eigenvals(mycca1, model = "constrained")
head(ev)

##       CCA1       CCA2       CCA3 
## 0.19308594 0.16271109 0.09060228

length(ev)

## [1] 3

Extracting axis scores

To extract a range of scores from a fitted ordination use scores()

• takes an ordination object as the first argument
• choices — which axes? Defaults to c(1,2)
• display — which type(s) of scores to return
  • "sites" or "wa": scores for samples in response matrix
  • "species": scores for variables/columns in response
  • "lc": linear combination site scores
  • "bp": biplot scores (coords of arrow tip)
  • "cn": centroid scores (coords of factor centroids)

Extracting axis scores

str(scores(cca1, choices = 1:4, display = c("species","sites")), max = 1)

## List of 2
##  $ species: num [1:44, 1:4] 0.0753 -0.1813 -1.0535 -1.2774 -0.1526 ...
##   ..- attr(*, "dimnames")=List of 2
##  $ sites  : num [1:24, 1:4] 0.178 -0.97 -1.28 -1.501 -0.598 ...
##   ..- attr(*, "dimnames")=List of 2

head(scores(cca1, choices = 1:2, display = "sites"))

##          CCA1       CCA2
## 18  0.1784733 -1.0598842
## 15 -0.9702382 -0.1971387
## 24 -1.2798478  0.4764498
## 27 -1.5009195  0.6521559
## 23 -0.5980933 -0.1840362
## 19 -0.1102881  0.7143142

Scalings…

When we draw the results of many ordinations we display 2 or more sets of data

Can't display all of these and maintain relationships between the scores

Solution scale one set of scores relative to the other via the scaling argument

Scalings…

• scaling = 1 — Focus on sites, scale site scores by λi${\lambda }_i$
• scaling = 2 — Focus on species, scale species scores by λi${\lambda }_i$
• scaling = 3 — Symmetric scaling, scale both scores by √λi$\sqrt{{\lambda }_i}$
• scaling = -1 — As above, but
• scaling = -2 — For cca() multiply results by √(1/(1−λi))$\sqrt{\left(1/\right(1-{\lambda }_i\left)\right)}$
• scaling = -3 — this is Hill's scaling
• scaling < 0 — For rda() divide species scores by species' σ$\sigma$
• scaling = 0 — raw scores

scores(cca1, choices = 1:2, display = "species", scaling = 3)

Scalings…

Thankfully we can use alternative descrpitors to extract scores:

• "none"
• "sites"
• "species"
• "symmetric"

Two modifiers select negative scores depending on whether the model is CCA or RDA:

• hill = TRUE
• correlation = TRUE

Example

• Using the CCA model you fitted, extract the site scores for axes 2 and 3 with Hill's scaling, focusing on the sites

scrs <- scores(mycca1, display = "sites", choices = c(2,3),
               scaling = "sites", hill = TRUE)
head(scrs)

##           CCA2        CCA3
## 18  0.21507383 -0.22617222
## 15 -0.53564592 -0.14736699
## 24 -0.28328352 -0.56306912
## 27 -0.79825273 -0.35205393
## 23 -0.06029273 -0.09438971
## 19  0.04742753  0.09586591

Partial constrained ordinations

Partial constrained ordinations remove the effect of one or more variables then fit model of interest

Argument Z is used for a data frame of variables to partial out

pcca <- cca(X = varespec,
            Y = varechem[, "Ca", drop = FALSE],
            Z = varechem[, "pH", drop = FALSE])

Or with the formula interface use the Condition() function

pcca <- cca(varespec ~ Ca + Condition(pH), data = varechem) ## easier!

Partial constrained ordinations

pcca <- cca(varespec ~ Ca + Condition(pH), data = varechem) ## easier!
pcca

## Call: cca(formula = varespec ~ Ca + Condition(pH), data = varechem)
## 
##               Inertia Proportion Rank
## Total          2.0832     1.0000     
## Conditional    0.1458     0.0700    1
## Constrained    0.1827     0.0877    1
## Unconstrained  1.7547     0.8423   21
## Inertia is scaled Chi-square 
## 
## Eigenvalues for constrained axes:
##    CCA1 
## 0.18269 
## 
## Eigenvalues for unconstrained axes:
##    CA1    CA2    CA3    CA4    CA5    CA6    CA7    CA8 
## 0.3834 0.2749 0.2123 0.1760 0.1701 0.1161 0.1089 0.0880 
## (Showing 8 of 21 unconstrained eigenvalues)

Triplots

plot(cca1)

Building constrained ordination models

If we don't want to think it's easy to fit a poor model with many constraints — That's what I did with cca1 and rda1

Remember, CCA and RDA are just regression methods — everything you know about regression applies here

A better approach is to think about the important variables and include only those

The formula interface allows you to create interaction or quadratic terms easily (though be careful with latter)

It also handles factor or class constraints automatically unlike the basic interface

Building constrained ordination models

vare.cca <- cca(varespec ~ Al + P*(K + Baresoil), data = varechem)
vare.cca

## Call: cca(formula = varespec ~ Al + P * (K + Baresoil), data =
## varechem)
## 
##               Inertia Proportion Rank
## Total           2.083      1.000     
## Constrained     1.046      0.502    6
## Unconstrained   1.038      0.498   17
## Inertia is scaled Chi-square 
## 
## Eigenvalues for constrained axes:
##   CCA1   CCA2   CCA3   CCA4   CCA5   CCA6 
## 0.3756 0.2342 0.1407 0.1323 0.1068 0.0561 
## 
## Eigenvalues for unconstrained axes:
##     CA1     CA2     CA3     CA4     CA5     CA6     CA7     CA8 
## 0.27577 0.15411 0.13536 0.11803 0.08887 0.05511 0.04919 0.03781 
## (Showing 8 of 17 unconstrained eigenvalues)

Building constrained ordination models

For CCA, RDA etc we have little choice but to do

1. Fit well-chosen set of candidate models & compare, or
2. Fit a full model of well-chosen variables & then do stepwise selection

Automatic approaches to model building should be used cautiously!

The standard step() function can be used as vegan provides two helper methods, deviance() and extractAIC(), used by step()

vegan also provides methods for class "cca" for add1() and drop1()

Variance inflation factors

Linear dependencies between constraints can be investigated with VIF

VIF is a measure of how much the variance of ˆβj${\hat{\beta }}_j$ is inflated by presence of other covariates

Lots of rules of thumb

• VIF >= 20 indicates strong collinearity in constraints
• VIF >= 10 potentially of concern & should be looked at

Computed via vif.cca()

vif.cca(cca1)

##         N         P         K        Ca        Mg         S        Al        Fe 
##  1.981742  6.028515 12.009357  9.925801  9.810609 18.378794 21.192739  9.127762 
##        Mn        Zn        Mo  Baresoil  Humdepth        pH 
##  5.380432  7.739664  4.320346  2.253683  6.012537  7.389267

Stepwise selection in CCA

step() uses AIC which is a fudge for RDA/CCA — use ordistep()

1. Define an upper and lower model scope, say the full model and the null model
2. To step from the lower scope or null model we use

upr <- cca(varespec ~ ., data = varechem)
lwr <- cca(varespec ~ 1, data = varechem)
set.seed(1)
mods <- ordistep(lwr, scope = formula(upr), trace = 0)

trace = 0 is used here to turn off printing of progress

Permutation tests are used (more on these later); the theory for an AIC for ordination is somewhat loose

Stepwise selection in CCA

The object returned by step() is a standard "cca" object with an extra component $anova

mods

## Call: cca(formula = varespec ~ Al + P + K, data = varechem)
## 
##               Inertia Proportion Rank
## Total          2.0832     1.0000     
## Constrained    0.6441     0.3092    3
## Unconstrained  1.4391     0.6908   20
## Inertia is scaled Chi-square 
## 
## Eigenvalues for constrained axes:
##   CCA1   CCA2   CCA3 
## 0.3616 0.1700 0.1126 
## 
## Eigenvalues for unconstrained axes:
##    CA1    CA2    CA3    CA4    CA5    CA6    CA7    CA8 
## 0.3500 0.2201 0.1851 0.1551 0.1351 0.1003 0.0773 0.0537 
## (Showing 8 of 20 unconstrained eigenvalues)

Stepwise selection in CCA

The $anova component contains a summary of the steps involved in automatic model building

mods$anova

##      Df    AIC      F Pr(>F)   
## + Al  1 128.61 3.6749  0.005 **
## + P   1 127.91 2.5001  0.005 **
## + K   1 127.44 2.1688  0.050 * 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

1. Al added first, then
2. P, followed by
3. K, then stopped

Stepwise selection in CCA

Step-wise model selection is fairly fragile; if we start from the full model we won't end up with the same final model

mods2 <- step(upr, scope = list(lower = formula(lwr), upper = formula(upr)), trace = 0,
              test = "perm")
mods2

Stepwise selection in CCA

mods2 <- step(upr, scope = list(lower = formula(lwr), upper = formula(upr)), trace = 0,
              test = "perm")
mods2

## Call: cca(formula = varespec ~ P + K + Mg + S + Mn + Mo + Baresoil +
## Humdepth, data = varechem)
## 
##               Inertia Proportion Rank
## Total          2.0832     1.0000     
## Constrained    1.1165     0.5360    8
## Unconstrained  0.9667     0.4640   15
## Inertia is scaled Chi-square 
## 
## Eigenvalues for constrained axes:
##   CCA1   CCA2   CCA3   CCA4   CCA5   CCA6   CCA7   CCA8 
## 0.4007 0.2488 0.1488 0.1266 0.0875 0.0661 0.0250 0.0130 
## 
## Eigenvalues for unconstrained axes:
##     CA1     CA2     CA3     CA4     CA5     CA6     CA7     CA8     CA9    CA10 
## 0.25821 0.18813 0.11927 0.10204 0.08791 0.06085 0.04461 0.02782 0.02691 0.01646 
##    CA11    CA12    CA13    CA14    CA15 
## 0.01364 0.00823 0.00655 0.00365 0.00238

Adjusted R2$R^2$ for ordination models

Ordinary R2$R^2$ is biased for the same reasons as for a linear regression

• adding a variable to constraints will increase R2$R^2$
• the larger the number of constraints in the model the larger R2$R^2$, is due to random correlations

Can attempt to account for this bias via an adjusted R2$R^2$ measure

Adjusted R2$R^2$ for ordination models

Can attempt to account for this bias via an adjusted R2$R^2$ measure

R2adj=1−n−1n−m−1(1−R2)$$R_{adj}^2=1-\frac{n-1}{n-m-1}(1-R^2)$$

• n$n$ is number of samples m$m$ is number of constraints (model degrees of freedom)
• Can be used up to ∼M>n/2$\sim M>n/2$ before becomes too conservative
• Can be negative

RsquareAdj(cca1)

## $r.squared
## [1] 0.6919576
## 
## $adj.r.squared
## [1] 0.2163163

Stepwise selection via adjusted R2$R^2$

Problems with stepwise selection are myriad. Affects RDA, CCA, etc

Blanchet et al (2008) proposed a two-step solution for models where R2adj$R_{adj}^2$ makes sense

Stepwise selection via adjusted R2$R^2$

• Global test of all constraints
  • Proceed only if this test is significant
  • Helps prevent inflation of overall type I error
• Proceed with forward selection, but with two stopping rules
  • Usual significance threshold α$\alpha$
  • The global R2adj$R_{adj}^2$
  • Stop if next candidate model is non-significant or if R2adj$R_{adj}^2$ exceeds the global R2adj$R_{adj}^2$

Available in ordiR2step()

Stepwise selection via adjusted R2$R^2$

ordiR2step(lwr, upr, trace = FALSE)

## Call: cca(formula = varespec ~ Al + P + K, data = varechem)
## 
##               Inertia Proportion Rank
## Total          2.0832     1.0000     
## Constrained    0.6441     0.3092    3
## Unconstrained  1.4391     0.6908   20
## Inertia is scaled Chi-square 
## 
## Eigenvalues for constrained axes:
##   CCA1   CCA2   CCA3 
## 0.3616 0.1700 0.1126 
## 
## Eigenvalues for unconstrained axes:
##    CA1    CA2    CA3    CA4    CA5    CA6    CA7    CA8 
## 0.3500 0.2201 0.1851 0.1551 0.1351 0.1003 0.0773 0.0537 
## (Showing 8 of 20 unconstrained eigenvalues)

Permutation tests in vegan

RDA has lots of theory behind it, CCA bit less. However, ecological/environmental data invariably violate what little theory we have

Instead we use permutation tests to assess the importance of fitted models — the data are shuffled in some way and the model refitted to derive a Null distribution under some hypothesis of no effect

Permutation tests in vegan

What is shuffled and how is of paramount importance for the test to be valid

• No conditioning (partial) variables then rows of the species data are permuted
• With conditioning variables, two options are available, both of which permute residuals from model fits
  • The full model uses residuals from model Y=X+Z+ε$Y=X+Z+\epsilon$
  • The reduced model uses residuals from model Y=Z+ε$Y=Z+\epsilon$
• In vegan which is used can be set via argument model with "direct", "full", and "reduced" respectively

Permutation tests in vegan

A test statistic is required, computed for observed model & each permuted model

vegan uses a pseudo F$F$ statistic

F=χ2model/dfmodelχ2resid/dfresid$$F=\frac{{\chi }_{model}^2/d{f}_{model}}{{\chi }_{resid}^2/d{f}_{resid}}$$

Evaluate whether F$F$ is unusually large relative to the null (permutation) distribution of F$F$

Permutation tests in vegan

pstat <- permustats(anova(cca1))
summary(pstat)

## 
##       statistic    SES   mean lower median  upper Pr(perm)  
## Model    1.4441 2.1270 1.0215       1.0033 1.3824    0.035 *
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## (Interval (Upper - Lower) = 0.95)

densityplot(pstat)

Permutation tests in vegan: anova()

• The main user function is the anova() method
• It is an interface to the lower-level function permutest.cca()
• At its most simplest, the anova() method tests whether the model as a whole is significant

Permutation tests in vegan: anova()

F=1.4415/140.6417/9=1.4441$$F=\frac{1.4415/14}{0.6417/9}=1.4441$$

set.seed(42)
(perm <- anova(cca1))

## Permutation test for cca under reduced model
## Permutation: free
## Number of permutations: 999
## 
## Model: cca(formula = varespec ~ N + P + K + Ca + Mg + S + Al + Fe + Mn + Zn + Mo + Baresoil + Humdepth + pH, data = varechem)
##          Df ChiSquare      F Pr(>F)  
## Model    14   1.44148 1.4441  0.029 *
## Residual  9   0.64171                
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Permutation tests in vegan: anova()

anova.cca() has a number of arguments

args(anova.cca)

## function (object, ..., permutations = how(nperm = 999), by = NULL, 
##     model = c("reduced", "direct", "full"), parallel = getOption("mc.cores"), 
##     strata = NULL, cutoff = 1, scope = NULL) 
## NULL

object is the fitted ordination

permutations controls what is permuted and how

by determines what is tested; the default is to test the model

Types of permutation test in vegan

A number of types of test can be envisaged

• Testing the overall significance of the model
• Testing constrained (canonical) axes
• Testing individual model terms sequentially
• The marginal effect of a single variable

The first is the default in anova()

The other three can be selected via the argument by

Testing canonical axes

• The constrained (canonical) axes can be individually tests by specifying by = "axis"
• The first axis is tested in terms of variance explained compared to residual variance
• The second axis is tested after partialling out the first axis…
• and so on

Testing canonical axes

set.seed(1)
anova(mods, by = "axis")

## Permutation test for cca under reduced model
## Forward tests for axes
## Permutation: free
## Number of permutations: 999
## 
## Model: cca(formula = varespec ~ Al + P + K, data = varechem)
##          Df ChiSquare      F Pr(>F)    
## CCA1      1   0.36156 5.0249  0.001 ***
## CCA2      1   0.16996 2.3621  0.034 *  
## CCA3      1   0.11262 1.5651  0.142    
## Residual 20   1.43906                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Testing terms sequentially

• The individual terms in the model can be tested using by = "terms"
• The terms are assessed in the order they were specified in the model, sequentially from first to last
• Test is of the additional variance explained by adding the kth variable to the model
• Ordering of the terms will affect the results

Testing terms sequentially

set.seed(5)
anova(mods, by = "terms")

## Permutation test for cca under reduced model
## Terms added sequentially (first to last)
## Permutation: free
## Number of permutations: 999
## 
## Model: cca(formula = varespec ~ Al + P + K, data = varechem)
##          Df ChiSquare      F Pr(>F)    
## Al        1   0.29817 4.1440  0.001 ***
## P         1   0.18991 2.6393  0.005 ** 
## K         1   0.15605 2.1688  0.018 *  
## Residual 20   1.43906                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Testing terms marginal effects

• The marginal effect of a model term can be assessed using by = "margin"
• The marginal effect is the effect of a particular term when all other model terms are included in the model

Testing terms marginal effects

set.seed(10)
anova(mods, by = "margin")

## Permutation test for cca under reduced model
## Marginal effects of terms
## Permutation: free
## Number of permutations: 999
## 
## Model: cca(formula = varespec ~ Al + P + K, data = varechem)
##          Df ChiSquare      F Pr(>F)    
## Al        1   0.31184 4.3340  0.001 ***
## P         1   0.16810 2.3362  0.016 *  
## K         1   0.15605 2.1688  0.029 *  
## Residual 20   1.43906                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Spring meadow vegetation

Example & data taken from Leps & Smilauer (2014), Case Study 2

Spring fen meadow vegetation in westernmost Carpathian mountains

## load vegan
library("vegan")
## load the data
spp <- read.csv("data/meadow-spp.csv", header = TRUE, row.names = 1)
env <- read.csv("data/meadow-env.csv", header = TRUE, row.names = 1)

Spring meadow vegetation

CCA a reasonable starting point as the gradient is long here (check with decorana() if you want)

m1 <- cca(spp ~ ., data = env)
set.seed(32)
anova(m1)

## Permutation test for cca under reduced model
## Permutation: free
## Number of permutations: 999
## 
## Model: cca(formula = spp ~ Ca + Mg + Fe + K + Na + Si + SO4 + PO4 + NO3 + NH3 + Cl + Corg + pH + conduct + slope, data = env)
##          Df ChiSquare     F Pr(>F)    
## Model    15    1.5597 1.497  0.001 ***
## Residual 54    3.7509                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Spring meadow vegetation

plot(m1)

Spring meadow vegetation

set.seed(67)
lwr <- cca(spp ~ 1, data = env)
( m2 <- ordistep(lwr, scope = formula(m1), trace = FALSE) )

## Call: cca(formula = spp ~ Ca + conduct + Corg + Na + NH3 + Fe + pH,
## data = env)
## 
##               Inertia Proportion Rank
## Total          5.3107     1.0000     
## Constrained    0.9899     0.1864    7
## Unconstrained  4.3208     0.8136   62
## Inertia is scaled Chi-square 
## 
## Eigenvalues for constrained axes:
##   CCA1   CCA2   CCA3   CCA4   CCA5   CCA6   CCA7 
## 0.4268 0.1447 0.1116 0.0936 0.0760 0.0719 0.0652 
## 
## Eigenvalues for unconstrained axes:
##     CA1     CA2     CA3     CA4     CA5     CA6     CA7     CA8 
## 0.27251 0.19518 0.16703 0.14993 0.14606 0.14168 0.13292 0.12154 
## (Showing 8 of 62 unconstrained eigenvalues)

Spring meadow vegetation

plot(m2)

Spring meadow vegetation

m2$anova

##           Df    AIC      F Pr(>F)   
## + Ca       1 453.14 4.7893  0.005 **
## + conduct  1 453.29 1.7915  0.005 **
## + Corg     1 453.61 1.6011  0.005 **
## + Na       1 453.93 1.5827  0.010 **
## + NH3      1 454.36 1.4507  0.020 * 
## + Fe       1 454.89 1.3386  0.040 * 
## + pH       1 455.46 1.2756  0.040 * 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Spring meadow vegetation

Alternative is RDA with a transformation

spph <- decostand(spp, method = "hellinger")
m3 <- rda(spph ~ ., data = env)
lwr <- rda(spph ~ 1, data = env)
m4 <- ordistep(lwr, scope = formula(m3),
               trace = FALSE)

m4

## Call: rda(formula = spph ~ Ca + NH3 + conduct + Si + Corg + NO3 + pH +
## Mg, data = env)
## 
##               Inertia Proportion Rank
## Total          0.6123     1.0000     
## Constrained    0.1823     0.2977    8
## Unconstrained  0.4300     0.7023   61
## Inertia is variance 
## 
## Eigenvalues for constrained axes:
##    RDA1    RDA2    RDA3    RDA4    RDA5    RDA6    RDA7    RDA8 
## 0.10572 0.02148 0.01224 0.01148 0.00945 0.00891 0.00696 0.00609 
## 
## Eigenvalues for unconstrained axes:
##     PC1     PC2     PC3     PC4     PC5     PC6     PC7     PC8 
## 0.04311 0.03026 0.02030 0.01767 0.01649 0.01519 0.01383 0.01346 
## (Showing 8 of 61 unconstrained eigenvalues)

Spring meadow vegetation

plot(m4)

Spring meadow vegetation

Stepwise using R2adj

m5 <- ordiR2step(lwr, scope = formula(m3), trace = FALSE)
m5$anova

##                  R2.adj Df     AIC       F Pr(>F)   
## + Ca            0.12588  1 -41.779 10.9370  0.002 **
## + NH3           0.14628  1 -42.468  2.6242  0.002 **
## + conduct       0.16322  1 -42.925  2.3570  0.002 **
## + Si            0.17711  1 -43.164  2.1136  0.002 **
## + Corg          0.18518  1 -42.940  1.6442  0.014 * 
## + NO3           0.19257  1 -42.680  1.5853  0.010 **
## + pH            0.19966  1 -42.417  1.5583  0.012 * 
## <All variables> 0.20332                             
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Restricted permutation tests

What is shuffled and how is of paramount importance for a valid test

Complete randomisation assumes a null hypothesis where all observations are independent

• Temporal or spatial correlation
• Clustering, repeated measures
• Nested sampling designs (Split-plots designs)
• Blocks
• …

Permutation must give null distribution of the test statistic whilst preserving the dependence between observations

Trick is to shuffle the data whilst preserving that dependence

Restricted permutations

Canoco has had restricted permutations for a long time. vegan has only recently caught up & we're not (quite) there yet

vegan used to only know how to completely randomise data or completely randomise within blocks (via strata in vegan)

The permute package grew out of initial code in the vegan repository to generate the sorts of restricted permutations available in Canoco

We have now fully integrated permute into vegan…

vegan depends on permute so it will already be installed & loaded when using vegan

Restricted permutations with permute

permute follows Canoco closely — at the (friendly!) chiding of Cajo ter Braak when it didn't do what he wanted!

Samples can be thought of as belonging to three levels of a hierarchy

• the sample level; how are individual samples permuted
• the plot level; how are samples grouped at an intermediate level
• the block level; how are samples grouped at the outermost level

Blocks define groups of plots, each of which can contain groups of samples

Restricted permutations with permute

Blocks are never permuted; if defined, only plots or samples within the blocks get shuffled & samples are never swapped between blocks

Plots or samples within plots, or both can be permuted following one of four simple permutation types

1. Free permutation (randomisation)
2. Time series or linear transect, equal spacing
3. Spatial grid designs, equal regular spacing
4. Permutation of plots (groups of samples)
5. Fixed (no permutation)

Multiple plots per block, multiple samples per plot; plots could be arranged in a spatial grid & samples within plots form time series

Blocks

Blocks are a random factor that does not interact with factors that vary within blocks

Blocks form groups of samples that are never permuted between blocks, only within blocks

Using blocks you can achieve what the strata argument used to in vegan; needs to be a factor variable

The variation between blocks should be excluded from the test; permute doesn't do this for you!

Use + Condition(blocks) in the model formula where blocks is a factor containing the block membership for each observation

Time series & linear transects

Can link randomly starting point of one series to any time point of another series if series are stationary under H₀ that series are unrelated

Achieve this via cyclic shift permutations — wrap series into a circle

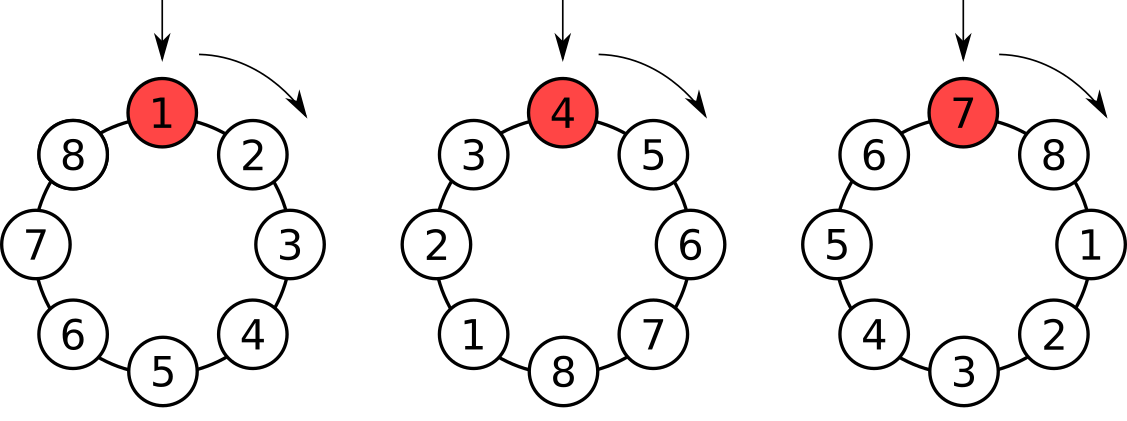
Time series & linear transects

Works OK if there are no trends or cyclic pattern — autocorrelation structure only broken at the end points if series are stationary

Can detrend to make series stationary but not if you want to test significance of a trend

shuffle(10, control = how(within = Within(type = "series")))

##  [1]  6  7  8  9 10  1  2  3  4  5

Spatial grids

set.seed(4)
h <- how(within = Within(type = "grid",
                         ncol = 3, nrow = 3))
perm <- shuffle(9, control = h)
matrix(perm, ncol = 3)

##      [,1] [,2] [,3]
## [1,]    1    4    7
## [2,]    2    5    8
## [3,]    3    6    9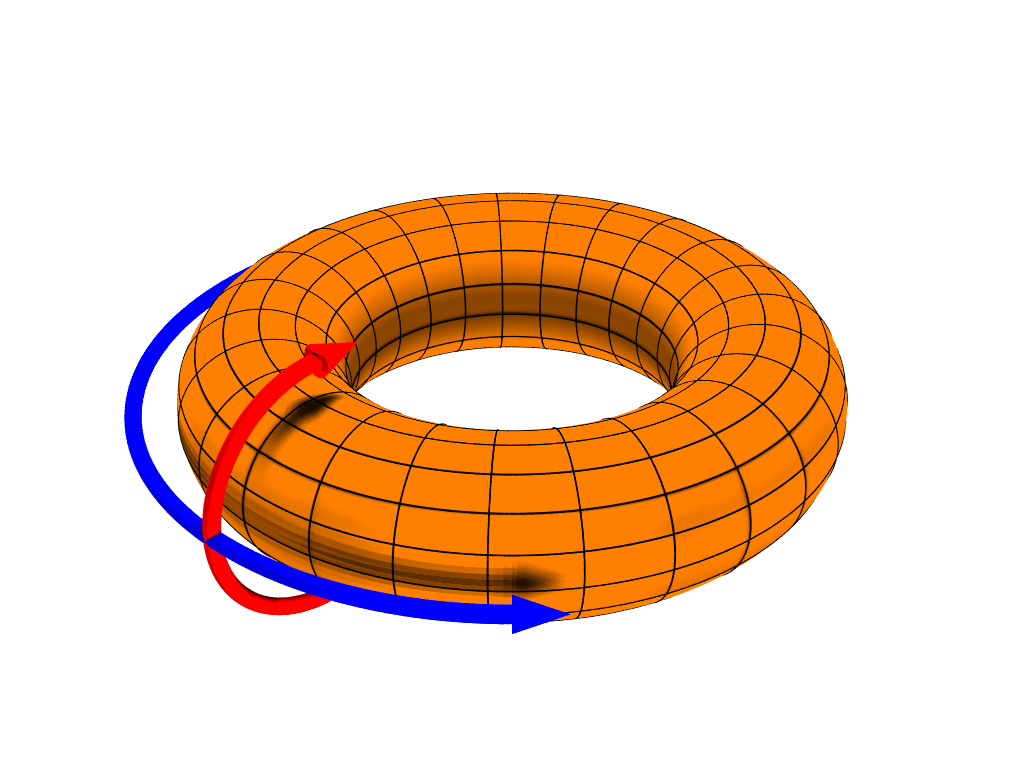

Whole-plots & split-plots I

Split-plot designs are hierarchical with two levels of units

1. whole-plots , which contain
2. split-plots (the samples)

Permute one or both, but whole-plots must be of equal size

Essentially allows more than one error stratum to be analyzed

Test effect of constraints that vary between whole plots by permuting the whole-plots whilst retaining order of split-splots (samples) within the whole-plots

Test effect of constraints that vary within whole-plots by permuting the split-plots within whole-plots without permuting the whole-plots

Whole-plots & split-plots II

Whole-plots or split-plots, or both, can be time series, linear transects or rectangular grids in which case the appropriate restricted permutation is used

If the split-plots are parallel time series & time is an autocorrelated error component affecting all series then the same cyclic shift can be applied to each time series (within each whole-plot) (constant = TRUE)

Mirrored permutations

Mirroring in restricted permutations allows for isotropy in dependencies by reflecting the ordering of samples in time or spatial dimensions

For a linear transect, technically the autocorrelation at lag h is equal to that at lag -h (also in a trend-free time series)

Mirrored permutations

Hence the series (1, 2, 3, 4) and (4, 3, 2, 1) are equivalent fom this point of view & we can draw permutations from either version

Similar argument can be made for spatial grids

Using mirror = TRUE then can double (time series, linear transects) or quadruple (spatial grids) the size of the set of permutations

Sets of permutations — no free lunch

Restricted severely reduce the size of the set of permutations

As the minimum p value obtainable is 1/np where np is number of allowed permutations (including the observed) this can impact the ability to detect signal/pattern

If we don't want mirroring

• in a time series of 20 samples the minimum p is 1/20 (0.05)
• in a time series of 100 samples the minimum p is 1/100 (0.01)
• in a data set with 10 time series each of 20 observations (200 total), if we assume an autocorrelated error component over all series (constant = TRUE) then there are only 20 permutations of the data and minimum p is 0.05

Sets of permutations — no free lunch

When the set of permutations is small it is better to switch to an exact test & evaluate all permutations in the set rather than randomly sample from the set

Use complete = TRUE in the call to how() — perhaps also increase maxperm

Designing permutation schemes

In permute, we set up a permutation scheme with how()

We sample from the permutation scheme with

• shuffle(), which gives a single draw from scheme, or
• shuffleSet(), which returns a set of n draws from the scheme

allPerms() can generated the entire set of permutations — note this was designed for small sets of permutations & is slow if you request it for a scheme with many thousands of permutations!

Designing permutation schemes

how() has three main arguments

1. within — takes input from helper Within()
2. plots — takes input from helper Plots()
3. blocks — takes a factor variable as input

plt <- gl(3, 10)
h <- how(within = Within(type = "series"), plots = Plots(strata = plt))

Designing permutation schemes

Helper functions make it easy to change one or a few aspects of permutation scheme, rest left at defaults

args(Within)

## function (type = c("free", "series", "grid", "none"), constant = FALSE, 
##     mirror = FALSE, ncol = NULL, nrow = NULL) 
## NULL

args(Plots)

## function (strata = NULL, type = c("none", "free", "series", "grid"), 
##     mirror = FALSE, ncol = NULL, nrow = NULL) 
## NULL

Designing permutation schemes

how() has additional arguments, many of which control the heuristics that kick in to stop you shooting yourself in the foot and demanding 9999 permutations when there are only 10

• complete should we enumerate the entire set of permutations?
• minperm lower bound on the size of the set of permutations at & below which we turn on complete enumeration

args(how)

## function (within = Within(), plots = Plots(), blocks = NULL, 
##     nperm = 199, complete = FALSE, maxperm = 9999, minperm = 5040, 
##     all.perms = NULL, make = TRUE, observed = FALSE) 
## NULL

Time series example I

Time series within 3 plots, 10 observation each

plt <- gl(3, 10)
h <- how(within = Within(type = "series"),
         plots = Plots(strata = plt))
set.seed(4)
p <- shuffle(30, control = h)
do.call("rbind", split(p, plt)) ## look at perms in context

##   [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## 1    9   10    1    2    3    4    5    6    7     8
## 2   14   15   16   17   18   19   20   11   12    13
## 3   24   25   26   27   28   29   30   21   22    23

Time series example II

Time series within 3 plots, 10 observation each, same permutation within each

plt <- gl(3, 10)
h <- how(within = Within(type = "series", constant = TRUE),
         plots = Plots(strata = plt))
set.seed(4)
p <- shuffle(30, control = h)
do.call("rbind", split(p, plt)) ## look at perms in context

##   [,1] [,2] [,3] [,4] [,5] [,6] [,7] [,8] [,9] [,10]
## 1    9   10    1    2    3    4    5    6    7     8
## 2   19   20   11   12   13   14   15   16   17    18
## 3   29   30   21   22   23   24   25   26   27    28

Restricted permutations | Ohraz

Now we've seen how to drive permute, we can use the same how() commands to set up permutation designs within vegan functions

Analyse the Ohraz data Case study 5 of Leps & Smilauer

Repeated observations of composition from an experiment

• Factorial design (3 replicates)
• Treatments: fertilisation, mowing, Molinia removal

Test 1 of the hypotheses

There are no directional changes in species composition in time that are common to all treatments or specific treatments

Restricted permutations | Ohraz

Analyse the Ohraz data Case study 5 of Leps & Smilauer

## load vegan
library("vegan")
## load the data
spp <- read.csv("data/ohraz-spp.csv", header = TRUE, row.names = 1)
env <- read.csv("data/ohraz-env.csv", header = TRUE, row.names = 1)
molinia <- spp[, 1]
spp <- spp[, -1]
## Year as numeric
env <- transform(env, year = as.numeric(as.character(year)))

Restricted permutations | Ohraz

c1 <- rda(spp ~ year + year:mowing + year:fertilizer + year:removal + Condition(plotid), data = env)
(h <- how(within = Within(type = "none"), plots = Plots(strata = env$plotid, type = "free")))

## 
## Permutation Design:
## 
## Blocks:
##   Defined by: none
## 
## Plots:
##   Plots: env$plotid
##   Permutation type: free
##   Mirrored?: No
## 
## Within Plots:
##   Permutation type: none
## 
## Permutation details:
##   Number of permutations: 199
##   Max. number of permutations allowed: 9999
##   Evaluate all permutations?: No.  Activation limit: 5040

Restricted permutations | Ohraz

set.seed(42)
anova(c1, permutations = h, model = "reduced")

## Permutation test for rda under reduced model
## Plots: env$plotid, plot permutation: free
## Permutation: none
## Number of permutations: 199
## 
## Model: rda(formula = spp ~ year + year:mowing + year:fertilizer + year:removal + Condition(plotid), data = env)
##          Df Variance      F Pr(>F)   
## Model     4   158.85 6.4247  0.005 **
## Residual 90   556.30                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Restricted permutations | Ohraz

set.seed(24)
anova(c1, permutations = h, model = "reduced", by = "axis")

## Permutation test for rda under reduced model
## Forward tests for axes
## Plots: env$plotid, plot permutation: free
## Permutation: none
## Number of permutations: 199
## 
## Model: rda(formula = spp ~ year + year:mowing + year:fertilizer + year:removal + Condition(plotid), data = env)
##          Df Variance       F Pr(>F)   
## RDA1      1    89.12 14.4173  0.005 **
## RDA2      1    34.28  5.5458  0.005 **
## RDA3      1    26.52  4.2900  0.025 * 
## RDA4      1     8.94  1.4458  0.485   
## Residual 90   556.30                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Hierarchical analysis of crayfish

Variation in communities may exist at various scales, sometimes hierarchically

A first step in understanding this variation is to test for its exisistence

In this example from Leps & Smilauer (2014) uses crayfish data from Spring River, Arkansas/Missouri, USA, collected by Dr. Camille Flinders.

567 records of 5 species, each sub-divided into Large & Small individuals

Hierarchical analysis of crayfish

## load data
crayfish <- head(read.csv("data/crayfish-spp.csv")[, -1], -1)
design <- read.csv("data/crayfish-design.csv", skip = 1)[, -1]
## fixup the names
names(crayfish) <- gsub("\\.", "", names(crayfish))
names(design) <- c("Watershed", "Stream", "Reach", "Run",
                   "Stream.Nested", "ReachNested", "Run.Nested")

Crayfish — Unconstrained

A number of samples have 0 crayfish, which excludes unimodal methods

m.pca <- rda(crayfish)
summary(eigenvals(m.pca))

## Importance of components:
##                          PC1    PC2    PC3    PC4     PC5     PC6     PC7
## Eigenvalue            3.5728 1.8007 1.1974 0.9012 0.79337 0.38886 0.28132
## Proportion Explained  0.3818 0.1924 0.1280 0.0963 0.08478 0.04155 0.03006
## Cumulative Proportion 0.3818 0.5742 0.7022 0.7985 0.88325 0.92480 0.95486
##                           PC8     PC9      PC10
## Eigenvalue            0.21225 0.20528 0.0048809
## Proportion Explained  0.02268 0.02194 0.0005216
## Cumulative Proportion 0.97754 0.99948 1.0000000

Crayfish — Unconstrained

layout(matrix(1:2, ncol = 2))
biplot(m.pca, type = c("text", "points"), scaling = "species")
set.seed(23)
ev.pca <- envfit(m.pca ~ Watershed, data = design, scaling = "species")
plot(ev.pca, labels = levels(design$Watershed), add = FALSE)
layout(1)

Crayfish — Watershed scale

m.ws <- rda(crayfish ~ Watershed, data = design)
m.ws

## Call: rda(formula = crayfish ~ Watershed, data = design)
## 
##               Inertia Proportion Rank
## Total          9.3580     1.0000     
## Constrained    1.7669     0.1888    6
## Unconstrained  7.5911     0.8112   10
## Inertia is variance 
## 
## Eigenvalues for constrained axes:
##   RDA1   RDA2   RDA3   RDA4   RDA5   RDA6 
## 0.7011 0.5540 0.3660 0.1064 0.0381 0.0013 
## 
## Eigenvalues for unconstrained axes:
##    PC1    PC2    PC3    PC4    PC5    PC6    PC7    PC8    PC9   PC10 
## 3.0957 1.2109 0.9717 0.7219 0.5333 0.3838 0.2772 0.2040 0.1879 0.0048

Crayfish — Watershed scale

summary(eigenvals(m.ws, constrained = TRUE))

## Importance of components:
##                         RDA1   RDA2   RDA3   RDA4    RDA5      RDA6
## Eigenvalue            0.7011 0.5540 0.3660 0.1064 0.03814 0.0012791
## Proportion Explained  0.3968 0.3135 0.2072 0.0602 0.02159 0.0007239
## Cumulative Proportion 0.3968 0.7103 0.9175 0.9777 0.99928 1.0000000

Crayfish — Watershed scale

set.seed(1)
ctrl <- how(nperm = 499, within = Within(type = "none"),
            plots = with(design, Plots(strata = Stream, type = "free")))
(sig.ws <- anova(m.ws, permutations = ctrl))

## Permutation test for rda under reduced model
## Plots: Stream, plot permutation: free
## Permutation: none
## Number of permutations: 499
## 
## Model: rda(formula = crayfish ~ Watershed, data = design)
##           Df Variance      F Pr(>F)   
## Model      6   1.7669 21.724  0.002 **
## Residual 560   7.5911                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Crayfish — Stream scale

m.str <- rda(crayfish ~ Stream + Condition(Watershed), data = design)
m.str

## Call: rda(formula = crayfish ~ Stream + Condition(Watershed), data =
## design)
## 
##               Inertia Proportion Rank
## Total          9.3580     1.0000     
## Conditional    1.7669     0.1888    6
## Constrained    1.1478     0.1227   10
## Unconstrained  6.4433     0.6885   10
## Inertia is variance 
## Some constraints were aliased because they were collinear (redundant)
## 
## Eigenvalues for constrained axes:
##   RDA1   RDA2   RDA3   RDA4   RDA5   RDA6   RDA7   RDA8   RDA9  RDA10 
## 0.4928 0.2990 0.2058 0.0782 0.0372 0.0224 0.0063 0.0030 0.0029 0.0002 
## 
## Eigenvalues for unconstrained axes:
##    PC1    PC2    PC3    PC4    PC5    PC6    PC7    PC8    PC9   PC10 
## 2.7853 0.8528 0.7737 0.6317 0.5144 0.2808 0.2517 0.1923 0.1559 0.0046

Crayfish — Stream scale

summary(eigenvals(m.str, constrained = TRUE))

## Importance of components:
##                         RDA1   RDA2   RDA3    RDA4    RDA5    RDA6     RDA7
## Eigenvalue            0.4928 0.2990 0.2058 0.07824 0.03719 0.02235 0.006326
## Proportion Explained  0.4293 0.2605 0.1793 0.06816 0.03240 0.01947 0.005511
## Cumulative Proportion 0.4293 0.6898 0.8691 0.93731 0.96971 0.98918 0.994694
##                           RDA8     RDA9     RDA10
## Eigenvalue            0.003042 0.002894 0.0001546
## Proportion Explained  0.002651 0.002521 0.0001347
## Cumulative Proportion 0.997344 0.999865 1.0000000

Crayfish — Stream scale

set.seed(1)
ctrl <- how(nperm = 499, within = Within(type = "none"),
            plots = with(design, Plots(strata = Reach, type = "free")),
            blocks = with(design, Watershed))
(sig.str <- anova(m.str, permutations = ctrl))

## Permutation test for rda under reduced model
## Blocks:  with(design, Watershed) 
## Plots: Reach, plot permutation: free
## Permutation: none
## Number of permutations: 499
## 
## Model: rda(formula = crayfish ~ Stream + Condition(Watershed), data = design)
##           Df Variance      F Pr(>F)   
## Model     14   1.1478 6.9477  0.004 **
## Residual 546   6.4433                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Crayfish — Reach scale

(m.re <- rda(crayfish ~ Reach + Condition(Stream), data = design))

## Call: rda(formula = crayfish ~ Reach + Condition(Stream), data =
## design)
## 
##               Inertia Proportion Rank
## Total          9.3580     1.0000     
## Conditional    2.9148     0.3115   20
## Constrained    1.4829     0.1585   10
## Unconstrained  4.9603     0.5301   10
## Inertia is variance 
## Some constraints were aliased because they were collinear (redundant)
## 
## Eigenvalues for constrained axes:
##   RDA1   RDA2   RDA3   RDA4   RDA5   RDA6   RDA7   RDA8   RDA9  RDA10 
## 0.6292 0.2706 0.2146 0.1414 0.1123 0.0467 0.0344 0.0270 0.0064 0.0003 
## 
## Eigenvalues for unconstrained axes:
##    PC1    PC2    PC3    PC4    PC5    PC6    PC7    PC8    PC9   PC10 
## 2.1635 0.6080 0.5605 0.5166 0.3749 0.2212 0.2052 0.1588 0.1477 0.0040

Crayfish — Reach scale

set.seed(1)
ctrl <- how(nperm = 499, within = Within(type = "none"),
            plots = with(design, Plots(strata = Run, type = "free")),
            blocks = with(design, Stream))
(sig.re <- anova(m.re, permutations = ctrl))

## Permutation test for rda under reduced model
## Blocks:  with(design, Stream) 
## Plots: Run, plot permutation: free
## Permutation: none
## Number of permutations: 499
## 
## Model: rda(formula = crayfish ~ Reach + Condition(Stream), data = design)
##           Df Variance      F Pr(>F)   
## Model     42   1.4829 3.5875  0.002 **
## Residual 504   4.9603                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Crayfish — Run scale

(m.run <- rda(crayfish ~ Run + Condition(Reach), data = design))

## Call: rda(formula = crayfish ~ Run + Condition(Reach), data = design)
## 
##               Inertia Proportion Rank
## Total          9.3580     1.0000     
## Conditional    4.3977     0.4699   62
## Constrained    1.8225     0.1948   10
## Unconstrained  3.1378     0.3353   10
## Inertia is variance 
## Some constraints were aliased because they were collinear (redundant)
## 
## Eigenvalues for constrained axes:
##   RDA1   RDA2   RDA3   RDA4   RDA5   RDA6   RDA7   RDA8   RDA9  RDA10 
## 0.8541 0.3141 0.1679 0.1393 0.1328 0.0835 0.0474 0.0429 0.0390 0.0016 
## 
## Eigenvalues for unconstrained axes:
##    PC1    PC2    PC3    PC4    PC5    PC6    PC7    PC8    PC9   PC10 
## 1.3137 0.4165 0.3832 0.2759 0.2378 0.1725 0.1215 0.1130 0.1016 0.0021

Crayfish — Run scale

set.seed(1)
ctrl <- how(nperm = 499, within = Within(type = "free"),
            blocks = with(design, Reach))
(sig.run <- anova(m.run, permutations = ctrl))

## Permutation test for rda under reduced model
## Blocks:  with(design, Reach) 
## Permutation: free
## Number of permutations: 499
## 
## Model: rda(formula = crayfish ~ Run + Condition(Reach), data = design)
##           Df Variance      F Pr(>F)   
## Model    126   1.8225 1.7425  0.002 **
## Residual 378   3.1378                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

MANOVA

MANOVA is the multivariate form of ANOVA

• Multivariate response data
• Categorical predictor variables

Decompose variation in the responses into

1. variation within groups
2. variation between groups

Test to see if two is unusually large relative to H₀

PERMANOVA

Doing that test requires lots of assumptions that rarely hold for ecological data

PERMANOVA: Permutational multivariate analysis of variance

Avoids most of these issues through the use of permutation tests

Directly decomposes a dissimilarity matrix into

1. variation within groups
2. variation between groups

PERMANOVA sensu stricto

vegan has four different ways to do essentially do this kind of analysis

1. adonis() — implements Anderson (2001)
2. adonis2() — implements McArdle & Anderson (2001)
3. dbrda() — implementation based on McArdle & Anderson (2001)
4. capscale() — implements Legendre & Anderson (1999)

Be careful with adonis() as it allows only sequential tests

A difference between the functions is how they treat negative eigenvalues

The PERMANOVA idea

PERMANOA — adonis2()

data(dune, dune.env)
adonis2(dune ~ Management*A1, data = dune.env, by = "terms")

## Permutation test for adonis under reduced model
## Terms added sequentially (first to last)
## Permutation: free
## Number of permutations: 999
## 
## adonis2(formula = dune ~ Management * A1, data = dune.env, by = "terms")
##               Df SumOfSqs      R2      F Pr(>F)   
## Management     3   1.4686 0.34161 3.2629  0.002 **
## A1             1   0.4409 0.10256 2.9387  0.020 * 
## Management:A1  3   0.5892 0.13705 1.3090  0.210   
## Residual      12   1.8004 0.41878                 
## Total         19   4.2990 1.00000                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

PERMANOA — adonis2()

data(dune, dune.env)
adonis2(dune ~ A1*Management, data = dune.env, by = "terms")

## Permutation test for adonis under reduced model
## Terms added sequentially (first to last)
## Permutation: free
## Number of permutations: 999
## 
## adonis2(formula = dune ~ A1 * Management, data = dune.env, by = "terms")
##               Df SumOfSqs      R2      F Pr(>F)    
## A1             1   0.7230 0.16817 4.8187  0.001 ***
## Management     3   1.1865 0.27600 2.6362  0.005 ** 
## A1:Management  3   0.5892 0.13705 1.3090  0.201    
## Residual      12   1.8004 0.41878                  
## Total         19   4.2990 1.00000                  
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

PERMANOA — adonis2()

data(dune, dune.env)
adonis2(dune ~ Management*A1, data = dune.env, by = "margin")

## Permutation test for adonis under reduced model
## Marginal effects of terms
## Permutation: free
## Number of permutations: 999
## 
## adonis2(formula = dune ~ Management * A1, data = dune.env, by = "margin")
##               Df SumOfSqs      R2     F Pr(>F)
## Management:A1  3   0.5892 0.13705 1.309  0.201
## Residual      12   1.8004 0.41878             
## Total         19   4.2990 1.00000

The interaction is the only term that isn't marginal to other terms; not significant

PERMANOA — adonis2()

adonis2(dune ~ Management + A1, data = dune.env, by = "margin")

## Permutation test for adonis under reduced model
## Marginal effects of terms
## Permutation: free
## Number of permutations: 999
## 
## adonis2(formula = dune ~ Management + A1, data = dune.env, by = "margin")
##            Df SumOfSqs      R2      F Pr(>F)   
## Management  3   1.1865 0.27600 2.4828  0.008 **
## A1          1   0.4409 0.10256 2.7676  0.020 * 
## Residual   15   2.3895 0.55583                 
## Total      19   4.2990 1.00000                 
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

The dispersion problem

Anderson (2001) noted that PERMANOVA could confound location & dispersion effects

If one or more groups are more variable — dispersed around the centroid — than the others, this can result in a false detection of a difference of means — a location effect

Same problem affects t tests, ANOVA

Warton et al (2012) Anderson & Walsh (2013) Anderson et al (2017)

Dispersion

Test for dispersion effects

Marti Anderson (2006) developed a test for multivariate dispersions — PERMDISP2

1. Calculate how far each observation is from its group median (or centroid)
2. Take the absolute values of these distances-to-medians
3. Do an ANOVA on the absolute distances with the groups as covariates
4. Test the H₀ of equal absolute distances to median among groups using a permutation test

In vegan this is betadisper()

Test for dispersion effects

data(varespec)
dis <- vegdist(varespec) # Bray-Curtis distances
## First 16 sites grazed, remaining 8 sites ungrazed
groups <- factor(c(rep(1,16), rep(2,8)),
                 labels = c("grazed","ungrazed"))
mod <- betadisper(dis, groups)
mod

## 
##     Homogeneity of multivariate dispersions
## 
## Call: betadisper(d = dis, group = groups)
## 
## No. of Positive Eigenvalues: 15
## No. of Negative Eigenvalues: 8
## 
## Average distance to median:
##   grazed ungrazed 
##   0.3926   0.2706 
## 
## Eigenvalues for PCoA axes:
## (Showing 8 of 23 eigenvalues)
##  PCoA1  PCoA2  PCoA3  PCoA4  PCoA5  PCoA6  PCoA7  PCoA8 
## 1.7552 1.1334 0.4429 0.3698 0.2454 0.1961 0.1751 0.1284

boxplot(mod)

Test for dispersions

set.seed(25)
permutest(mod)

## 
## Permutation test for homogeneity of multivariate dispersions
## Permutation: free
## Number of permutations: 999
## 
## Response: Distances
##           Df  Sum Sq  Mean Sq      F N.Perm Pr(>F)  
## Groups     1 0.07931 0.079306 4.6156    999  0.045 *
## Residuals 22 0.37801 0.017182                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

plot(mod)

Test for dispersions

set.seed(4)
permutest(mod, pairwise = TRUE)

## 
## Permutation test for homogeneity of multivariate dispersions
## Permutation: free
## Number of permutations: 999
## 
## Response: Distances
##           Df  Sum Sq  Mean Sq      F N.Perm Pr(>F)  
## Groups     1 0.07931 0.079306 4.6156    999  0.036 *
## Residuals 22 0.37801 0.017182                       
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Pairwise comparisons:
## (Observed p-value below diagonal, permuted p-value above diagonal)
##           grazed ungrazed
## grazed              0.043
## ungrazed 0.04295

Test for locations with non-equal dispersion?

Marti Anderson & colleagues (2017) have proposed a solution that is related to the Berens-Fisher problem

This is in Primer but not yet in vegan

https://github.com/vegandevs/vegan/issues/344

Diagnostics for constrained ordinations

vegan provides a series of diagnostics to help assess the model fit

• goodness()
• inertcomp()
• spenvcor()
• intersetcor()
• vif.caa()

Diagnostics | goodness of fit

goodness() computes a goodness of fit statistic for species or sites, controlled by argument display

Gives the cumulative proportion of variance explained by each axis

head(goodness(mods))

##                  CCA1        CCA2      CCA3
## Callvulg 0.0062471656 0.318907619 0.8254657
## Empenigr 0.1164701677 0.137604904 0.1953245
## Rhodtome 0.0999089739 0.169697909 0.1824153
## Vaccmyrt 0.2361482843 0.240516323 0.2406730
## Vaccviti 0.1523704591 0.156502301 0.2110550
## Pinusylv 0.0009244423 0.004802076 0.0060096

Diagnostics | inertia decomposition

inertcomp() decomposes the variance in samples or species in partial, constrained, and unconstrained components

• statistic = "explained (default) gives the decomposition in terms of variance
• statistic = "distance" gives decomposition in terms of the the residual distance

head(inertcomp(mods, proportional = TRUE))

##                CCA        CA
## Callvulg 0.8254657 0.1745343
## Empenigr 0.1953245 0.8046755
## Rhodtome 0.1824153 0.8175847
## Vaccmyrt 0.2406730 0.7593270
## Vaccviti 0.2110550 0.7889450
## Pinusylv 0.0060096 0.9939904

Diagnostics | species-environment correlations

spenvcor() returns the (weighted) correlation between the weighted average-based and the linear combination-based sets of site scores

A poor measure of goodness of fit. Sensitive to

• outliers (like all correlations)
• overfitting (using too many constraints)

Better models can have poorer species-environment correlations

spenvcor(mods)

##      CCA1      CCA2      CCA3 
## 0.8554793 0.8131627 0.8792221

Diagnostics | interset correlations

intersetcor() returns the (weighted) correlation between the weighted average-based site scores and each constraint variable

Another poor diagnostic

• correlation based
• focuses on a single constraint--axis combination at a time

intersetcor(mods)

##          CCA1       CCA2      CCA3
## Al  0.7356445 -0.1304293 0.4260453
## P  -0.3588931 -0.6109601 0.4478786
## K  -0.3767902 -0.1339051 0.7759566

Vector fitting (envfit()) or biplot scores (scores(model, display = "bp")) are better alternatives

Links

I have several vegan-related posts on my blog.

For a list of posts see http://www.fromthebottomoftheheap.net/blog/

Acknowledgments

Slides

• HTML Slide deck bit.ly/adv-vegan © Simpson (2020)
• RMarkdown Source

References